Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-06-19T22:10:46.704Z Has data issue: false hasContentIssue false
  • English
  • Français

Beurling-Dahlberg-Sjögren Type Theorems for Minimally Thin Sets in a Cone

Published online by Cambridge University Press:  20 November 2018

Ikuko Miyamoto ,
Minoru Yanagishita  and
Hidenobu Yoshida
Ikuko Miyamoto
Affiliation:
Department of Mathematics and Informatics, Faculty of Science, Chiba University, 1-33 Yayoi-cho, Inage-ku, Chiba 263-8522, Japan, email: miyamoto@math.s.chiba-u.ac.jpmyanagis@g.math.s.chiba-u.ac.jpyoshida@math.s.chiba-u.ac.jp
Minoru Yanagishita
Affiliation:
Department of Mathematics and Informatics, Faculty of Science, Chiba University, 1-33 Yayoi-cho, Inage-ku, Chiba 263-8522, Japan, email: miyamoto@math.s.chiba-u.ac.jpmyanagis@g.math.s.chiba-u.ac.jpyoshida@math.s.chiba-u.ac.jp
Hidenobu Yoshida
Affiliation:
Department of Mathematics and Informatics, Faculty of Science, Chiba University, 1-33 Yayoi-cho, Inage-ku, Chiba 263-8522, Japan, email: miyamoto@math.s.chiba-u.ac.jpmyanagis@g.math.s.chiba-u.ac.jpyoshida@math.s.chiba-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper shows that some characterizations of minimally thin sets connected with a domain having smooth boundary and a half-space in particular also hold for the minimally thin sets at a corner point of a special domain with corners, i.e., the minimally thin set at 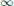$\infty$ of a cone.

Keywords

31B0531B20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 2 , 01 June 2003 , pp. 252 - 264
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Aikawa, H., Quasiadditivity of Riesz capacity. Math. Scand. 69 (1991), 15–30.Google Scholar
[2] Aikawa, H., Quasiadditivity of capacity and minimal thinness. Ann. Acad. Sci. Fenn.Math. Ser. AI 18 (1993), 65–75.Google Scholar
[3] Aikawa, H. and Essén, M., Potential Theory-Selected Topics. Lecture Notes in Math. 1633, Springer-Verlag, 1996.Google Scholar
[4] Ancona, A., On strong barriers and an inequality of Hardy for domains in Rn. J. LondonMath. Soc. (2) 34 (1986), 274–290.Google Scholar
[5] Azarin, V. S., Generalization of a theorem of Hayman on subharmonic functions in an m-dimensional cone. Mat. Sb. 66 (108)(1965), 248–264; Amer.Math. Soc. Transl. (2) 80 (1969), 119–138.Google Scholar
[6] Beurling, A., A minimum principle for positive harmonic functions. Ann. Acad. Sci. Fenn. Ser. AI. Math. 372, 1965.Google Scholar
[7] Brelot, M., On topologies and boundaries in potential theory. Lecture Notes in Math. 175, Springer-Verlag, 1971.Google Scholar
[8] Courant, R. and Hilbert, D., Methods of mathematical physics. 1st English edition, Interscience, New York, 1954.Google Scholar
[9] Dahlberg, B. E. J., A minimum principle for positive harmonic functions. Proc. London Math. Soc. (3) 33 (1976), 238–250.Google Scholar
[10] Doob, J. I., Classical potential theory and its probabilistic counterpart. Springer-Verlag, 1984.Google Scholar
[11] Essén, M. and Jackson, H. L., On the covering properties of certain exceptional sets in a half-space. Hiroshima Math. J. 10 (1980), 233–262.Google Scholar
[12] Gilbarg, D. and Trudinger, N. S., Elliptic partial differential equations of second order. Springer-Verlag, Berlin, 1977.Google Scholar
[13] Helms, L. L., Introduction to potential theory. Wiley, New York, 1969.Google Scholar
[14] Lewis, J. L., Uniformly fat sets. Trans. Amer.Math. Soc. 308 (1988), 177–196.Google Scholar
[15] Miyamoto, I. and Yoshida, H., Two criteria of Wiener type for minimally thin sets and rareèd sets in a cone. J. Math. Soc. Japan, to appear.Google Scholar
[16] Sjögren, P., Une propriété des fonctions harmoniques positives d'après Dahlberg. In: Séminaire de théorie du potentiel, Lecture Notes in Math. 563, Springer, Berlin, 1976, 275–282.Google Scholar
[17] Stein, E. M., Singular integrals and differentiability properties of functions. Princeton University Press, 1970.Google Scholar