Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-26T21:50:30.142Z Has data issue: false hasContentIssue false
  • English
  • Français

An Infinite Dimensional Vector Space of Universal Functions for H∞ of the Ball

Published online by Cambridge University Press:  20 November 2018

Richard Aron  and
Pamela Gorkin
Richard Aron
Affiliation:
Department of Mathematical Sciences, Kent State University, Kent, OH 44242, U.S.A. e-mail: aron@math.kent.edu
Pamela Gorkin
Affiliation:
Department of Mathematics, Bucknell University, Lewisburg, PA 17837, U.S.A. e-mail: pgorkin@bucknell.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that there exists a closed infinite dimensional subspace of 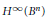${{H}^{\infty }}\left( {{B}^{n}} \right)$ such that every function of norm one is universal for some sequence of automorphisms of 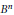${{B}^{n}}$.

Keywords

47B3847B3346J10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 2 , 01 June 2007 , pp. 172 - 181
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Axler, S. and Gorkin, P., Sequences in the maximal ideal space of H∞ . Proc. Amer. Math. Soc. 108(1990), no. 3, 731–740.Google Scholar
[2] Bayart, F., Universal inner functions on the ball. To appear, Canad. Math. Bull.Google Scholar
[3] Bernal-González, L. and Montes-Rodríguez, A., Non-finite-dimensional closed vector spaces of universal functions for composition operators. J. Approx. Theory 82(1995), no. 3, 375–391.Google Scholar
[4] Birkhoff, G. D., Démonstration d’un théorème élémentaire sur les fonctions entiéres. C. R. Acad. Sci. Paris 189(1929), 473–475.Google Scholar
[5] Chee, P. S., Universal functions in several complex variables. J. Austral. Math. Soc. Ser. A 28(1979), no. 2, 189–196.Google Scholar
[6] Gauthier, P. M. and Xiao, J., The existence of universal inner functions on the unit ball of Cn . Canad. Math. Bull. 49(2005), no. 3, 409–413.Google Scholar
[7] Gorkin, P. and Mortini, R. Asymptotic interpolating sequences in uniform algebras. J. London Math. Soc. (2) 67(2003), no. 2, 481–498.Google Scholar
[8] Gorkin, P. and Mortini, R., Universal Blaschke products. Math. Proc. Cambridge Philos. Soc. 136(2004), no. 1, 175–184.Google Scholar
[9] Gorkin, P. and Mortini, R., Universal singular inner functions. Canad. Math. Bull. 47(2004), no. 1, 17–21.Google Scholar
[10] Grosse-Erdmann, K.-G., Universal families and hypercyclic operators. Bull. Amer. Math. Soc. (N.S.) 36(1999), no. 3, 345–381.Google Scholar
[11] Heins, M., A universal Blaschke product. Archiv Math. 6(1954), 41–44.Google Scholar
[12] Hosokawa, T., Izuchi, K., and Zheng, D., Isolated points and essential components of composition operators on H∞ . Proc. Amer. Math. Soc. 130(2002), no. 6, 1765–1773 (electronic).Google Scholar
[13] Montes-Rodríguez, A., Vector spaces of universal functions. In: Complex methods in approximation theory. Monogr. Cienc. Tecnol. 2, Universidad Almería, Almería, 1997, pp. 113–116,.Google Scholar
[14] Montes-Rodríguez, A., A note on Birkhoff open sets. Complex Variables Theory Appl. 30(1996), no. 3, 193–198.Google Scholar
[15] Mortini, R., Infinite dimensional universal subspaces generated by Blaschke products. Proc. Amer. Math. Soc. 135(2007), no. 6, 1795–1801.Google Scholar
[16] Rudin, W., Function theory in the unit ball of Cn. Grundlehren der Mathematischen Wissenschaften 241. Springer-Verlag, New York, 1980.Google Scholar
[17] Seidel, W. and Walsh, J. L., On approximation by euclidean and non-euclidean translations of an analytic function. Bull. Amer. Math. Soc. 47(1941), 916–920.Google Scholar