No CrossRef data available.
Article contents
On the average value of 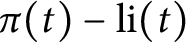 $\pi (t)-\operatorname {\textrm {li}}(t)$
$\pi (t)-\operatorname {\textrm {li}}(t)$
Published online by Cambridge University Press: 14 March 2022
Abstract
We prove that the Riemann hypothesis is equivalent to the condition
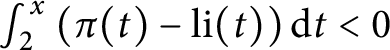 $\int _{2}^x\left (\pi (t)-\operatorname {\textrm {li}}(t)\right )\textrm {d}t<0$
for all
$\int _{2}^x\left (\pi (t)-\operatorname {\textrm {li}}(t)\right )\textrm {d}t<0$
for all
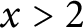 $x>2$
. Here,
$x>2$
. Here,
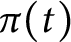 $\pi (t)$
is the prime-counting function and
$\pi (t)$
is the prime-counting function and
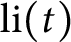 $\operatorname {\textrm {li}}(t)$
is the logarithmic integral. This makes explicit a claim of Pintz. Moreover, we prove an analogous result for the Chebyshev function
$\operatorname {\textrm {li}}(t)$
is the logarithmic integral. This makes explicit a claim of Pintz. Moreover, we prove an analogous result for the Chebyshev function
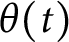 $\theta (t)$
and discuss the extent to which one can make related claims unconditionally.
$\theta (t)$
and discuss the extent to which one can make related claims unconditionally.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society, 2022





