Research Article
Some Supercuspidal Representations of Sp4(k)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-7
-
- Article
-
- You have access
- Export citation
Colour Switching and Homeomorphism of Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 8-32
-
- Article
-
- You have access
- Export citation
Operators on L2(I) ⊕ Cr
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 33-53
-
- Article
-
- You have access
- Export citation
A Variation of the Koebe Mapping in a Dense Subset of S
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 54-73
-
- Article
-
- You have access
- Export citation
Analytic Subalgebras of Von Neumann Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 74-99
-
- Article
-
- You have access
- Export citation
Dirac Systems with Discrete Spectra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 100-122
-
- Article
-
- You have access
- Export citation
Multipliers for Amalgams and the Algebra S0(G)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 123-148
-
- Article
-
- You have access
- Export citation
Characters of Non-Connected, Reductive p-Abic Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 149-167
-
- Article
-
- You have access
- Export citation
On Representations of Grothendieck Toposes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 168-221
-
- Article
-
- You have access
- Export citation
Frobenius Induction for Higher Whitehead Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 222-238
-
- Article
-
- You have access
- Export citation
High Level Occupation Times for Gaussian Stochastic Processes with Sample Paths in Orlicz Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 239-256
-
- Article
-
- You have access
- Export citation

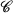 is the colour set, for each
is the colour set, for each 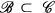 we set
we set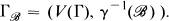
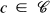 set
set 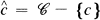 . For
. For 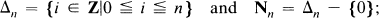
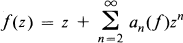
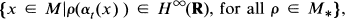
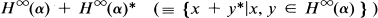
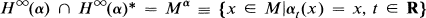
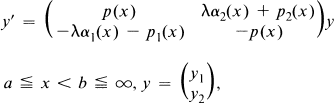
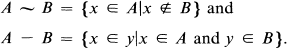
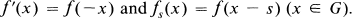
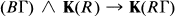
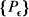 a family of probability measures on the Borel subsets of
a family of probability measures on the Borel subsets of