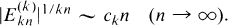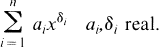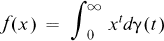Research Article
Groupoid Enriched Categories and Homotopy Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-416
-
- Article
-
- You have access
- Export citation
The Enumeration of Non-Isomorphic 2-Connected Planar Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-435
-
- Article
-
- You have access
- Export citation
Asymptotic Behaviour of Nonoscillatory Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 436-453
-
- Article
-
- You have access
- Export citation
Local Stability and Saturation in Spaces of Orderings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 454-477
-
- Article
-
- You have access
- Export citation
The Hilbert Transform of Generalized Functions and Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 478-495
-
- Article
-
- You have access
- Export citation
Representations of Well-Founded Preference Orders
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 496-508
-
- Article
-
- You have access
- Export citation
Polynomials with Coefficients from a Division Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 509-515
-
- Article
-
- You have access
- Export citation
The Metric Fuglede Property and Normality
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 516-525
-
- Article
-
- You have access
- Export citation
Generalized Euler Number Sequences: Asymptotic Estimates and Congruences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 526-546
-
- Article
-
- You have access
- Export citation
Uniform Approximation by Polynomials with Variable Exponents
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 547-557
-
- Article
-
- You have access
- Export citation
Homomorphism-Compact Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 558-576
-
- Article
-
- You have access
- Export citation

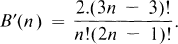
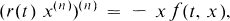
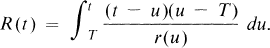
 which is transitive, reflexive and total. This preorder partitions the set
which is transitive, reflexive and total. This preorder partitions the set 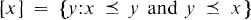 . The natural relation induced by
. The natural relation induced by 
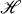 , that
, that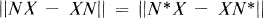
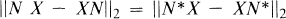
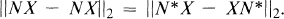
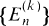 one for each positive integer
one for each positive integer 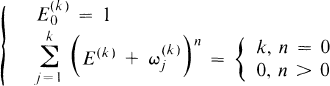
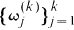 are the
are the 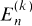 after multiplying out. We note that (1.1) implies
after multiplying out. We note that (1.1) implies 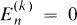 ,
, 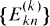 by showing that
by showing that