Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Berndt, Bruce C.
2001.
Special Functions 2000: Current Perspective and Future Directions.
p.
61.
Jorgenson, Jay
and
O’Sullivan, Cormac
2005.
Convolution Dirichlet Series and a Kronecker Limit Formula for Second-Order Eisenstein Series.
Nagoya Mathematical Journal,
Vol. 179,
Issue. ,
p.
47.
Chapman, Robin
and
Hart, William
2006.
Evaluation of the Dedekind Eta Function.
Canadian Mathematical Bulletin,
Vol. 49,
Issue. 1,
p.
21.
Doyle, Greg
and
Williams, Kenneth S.
2018.
Evaluation of some q-integrals in terms of the Dedekind eta function.
Analysis,
Vol. 38,
Issue. 2,
p.
63.
Boysal, Arzu
Ecevit, Fatih
and
Yıldırım, Cem Yalçın
2018.
A lattice sum involving the cosine function.
Journal of Mathematical Analysis and Applications,
Vol. 463,
Issue. 1,
p.
134.
Chen, Parry Y.
Smith, Michael J. A.
and
McPhedran, Ross C.
2018.
Evaluation and regularization of phase-modulated Eisenstein series and application to double Schlömilch-type sums.
Journal of Mathematical Physics,
Vol. 59,
Issue. 7,
Dawsey, Madeline Locus
and
Ono, Ken
2019.
Elliptic Integrals, Elliptic Functions and Modular Forms in Quantum Field Theory.
p.
183.
Bhattacharya, Soumya
2019.
Finiteness of irreducible holomorphic eta quotients of a given level.
The Ramanujan Journal,
Vol. 48,
Issue. 2,
p.
423.
Ono, Ken
2021.
From Operator Theory to Orthogonal Polynomials, Combinatorics, and Number Theory.
Vol. 285,
Issue. ,
p.
371.
Bringmann, Kathrin
Ono, Ken
and
Wagner, Ian
2023.
Eichler integrals of Eisenstein series as q-brackets of weighted t-hook functions on partitions.
The Ramanujan Journal,
Vol. 61,
Issue. 1,
p.
279.
Babei, Angelica
Beneish, Lea
Roy, Manami
Swisher, Holly
Tobin, Bella
and
Tu, Fang-Ting
2024.
Research Directions in Number Theory.
Vol. 33,
Issue. ,
p.
87.
 $d$ be the discriminant of an imaginary quadratic field. Let
$d$ be the discriminant of an imaginary quadratic field. Let  $a$,
$a$, 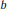 $b$,
$b$,  $c$ be integers such that
$c$ be integers such that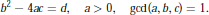 $${{b}^{2}}-4ac=d,a>0,\gcd (a,b,c)=1.$$
$${{b}^{2}}-4ac=d,a>0,\gcd (a,b,c)=1.$$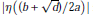 $\left| \eta ((b+\sqrt{d})/\left. 2a) \right| \right.$ is determined explicitly, where
$\left| \eta ((b+\sqrt{d})/\left. 2a) \right| \right.$ is determined explicitly, where 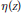 $\eta \left( z \right)$ is Dedekind’s eta function
$\eta \left( z \right)$ is Dedekind’s eta function $$\eta (z)\,=\,{{e}^{\pi iz/12}}\,\prod\limits_{m=1}^{\infty }{(1-{{e}^{2\pi imz}})\,\,\,(im(z)>0).}$$
$$\eta (z)\,=\,{{e}^{\pi iz/12}}\,\prod\limits_{m=1}^{\infty }{(1-{{e}^{2\pi imz}})\,\,\,(im(z)>0).}$$



