Soit 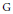$\text{G}$ un groupe réductif 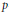$p$-adique, et soit 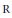$\text{R}$ un corps algébriquement clos. Soit 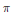$\text{ }\!\!\pi\!\!\text{ }$ une représentation lisse de 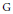$\text{G}$ dans un espace vectoriel 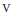$\text{V}$ sur 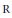$\text{R}$. Fixons un sous-groupe ouvert et compact 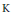$\text{K}$ de 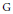$\text{G}$ et une représentation lisse irréductible 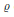$\varrho$ de 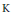$\text{K}$ dans un espace vectoriel 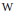$\text{W}$ de dimension finie sur 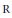$\text{R}$. Sur l'espace 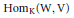$\text{Ho}{{\text{m}}_{\text{K}}}(\text{W,}\,\text{V)}$ agit l'algèbre d'entrelacement 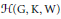$\mathcal{H}(\text{G,}\,\text{K,}\,\text{W)}$. Nous examinons la compatibilité de ces constructions avec le passage aux représentations contragrédientes 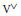${{\text{V}}^{\vee }}$ et 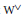${{\text{W}}^{\vee }}$, et donnons en particulier des conditions sur 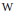$\text{W}$ ou sur la caractéristique de 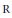$\text{R}$ pour que le comportement soit semblable au cas des représentations complexes. Nous prenons un point de vue abstrait, n'utilisant que des propriétés générales de 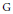$\text{G}$. Nous terminons par une application á la théorie des types pour le groupe 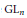$\text{G}{{\text{L}}_{n}}$ et ses formes intérieures sur un corps local non archimédien.