Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-06-03T00:30:45.004Z Has data issue: false hasContentIssue false
  • English
  • Français

A Tauberian Theorem of Exponential Type

Published online by Cambridge University Press:  20 November 2018

J. L. Geluk ,
L. de Haan  and
U. Stadtmüller
J. L. Geluk
Affiliation:
Erasmus Universiteit, Rotterdam, Netherlands
L. de Haan
Affiliation:
Universität Ulm, Ulm, West Germany
U. Stadtmüller
Affiliation:
Universität Ulm, Ulm, West Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. We will be interested in Tauberian theorems concerning the limiting behaviour of a monotone function U and its Laplace transform

A famous theorem of Karamata concerns the case in which the function U is regularly varying (i.e., U(tx)/U(t) → xα(t → ∞) for x > 0). Here we will consider functions U that grow faster, in fact our conditions will be in terms of log U rather than on U itself. So it is convenient to write the Laplace transform in terms of q = log U. For a function q:R+ → R such that exp q is locally integrable and

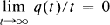
we define the function 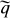by the relation

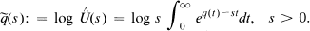
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 3 , 01 June 1986 , pp. 697 - 718
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Aljancić, S. and Arandelović, D., 0-regularly varying functions, Publ. de l'Inst. Math. Beograd 22 (1977), 5–22.Google Scholar
2. Balkema, A. A., Geluk, J. L. and de Haan, L., An extension of Karamatas Tauberian theorem and its connection with complementary convex functions, Quart. J. Math. Oxford (2) 30 (1979), 385–416.Google Scholar
3. Balkema, A. A. and Haan, L. de, On R. von Mises’ condition for the domain of attraction of exp(–e–x), Ann. Math. Stat. 43 (1972), 1352–1354.Google Scholar
4. Geluk, J. L., On regular variation and its applications in number theory, Ph. D. thesis, University of Leiden (1983).Google Scholar
5. Haan, L. de, On regular variation and its application to the weak convergence of sample extremes, Math. Centre Tracts 32 (Amsterdam, 1970).Google Scholar
6. Haan, L. de and Resnick, S. I., Stochastic processes and point processes, Report 8136/S, Econometric Inst., Erasmus University (1981).Google Scholar
7. Haan, L. de and Resnick, S. I., Asymptotically balanced functions and stochastic compactness of sample extremes, Ann. Prob. (1984), to appear.CrossRefGoogle Scholar
8. Haan, L. de and Stadtmüller, U., Dominated variation and related concepts and Tauberian theorems for Laplace transforms, J. Math. Anal. Appl. 108 (1985), 344–365.Google Scholar
9. Kohlbecker, E. E., Weak asymptotic properties of partitions, Trans. Amer. Math. Soc. 88 (1958), 346–365.Google Scholar
10. Korevaar, J., Aardenne-Ehrenfest, T. van and de Bruijn, N. G., A note on slowly oscillating functions, Nw. Arch. Wisk. 23 (1949), 77–86.Google Scholar
11. Krasnosel'skii, M. A. and Rutickii, Ya. B., Convex functions and Orlicz spaces (Noordhoff, Groningen, 1961).Google Scholar
12. Wagner, E., Ein reeller Tauberscher Satzfur die Lap lace-Transformation, Math. Nachr. 36 (1968), 323–331.Google Scholar