Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-07-06T11:32:18.505Z Has data issue: false hasContentIssue false
  • English
  • Français

Spaces of Whitney Functions on Cantor-Type Sets

Published online by Cambridge University Press:  20 November 2018

Bora Arslan ,
Alexander P. Goncharov  and
Mefharet Kocatepe
Bora Arslan
Affiliation:
Bilkent University Department of Mathematics 06533 Bilkent Ankara Turkey, email: barslan@firstlinux.net
Alexander P. Goncharov
Affiliation:
Bilkent University Department of Mathematics 06533 Bilkent Ankara Turkey, email: goncha@fen.bilkent.edu.tr
Mefharet Kocatepe
Affiliation:
Bilkent University Department of Mathematics 06533 Bilkent Ankara Turkey, email: kocatepe@fen.bilkent.edu.tr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce the concept of logarithmic dimension of a compact set. In terms of this magnitude, the extension property and the diametral dimension of spaces 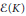$\varepsilon \left( K \right)$ can be described for Cantor-type compact sets.

Keywords

46E1031A1546A04
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 2 , 01 April 2002 , pp. 225 - 238
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Bessaga, C., Pelczyński, A. and Rolewicz, S., On Diametral approximative dimension and linear homogeneity of F-spaces. Bull. Acad. Pol. Sci. 9 (1961), 677–683.Google Scholar
[2] Bierstone, E., Extension of Whitney-Fields from Subanalytic Sets. Invent. Math. 46 (1978), 277–300.Google Scholar
[3] Falconer, K., Fractal Geometry, Mathematical Foundations and Applications. John Wiley & Sons, 1990.Google Scholar
[4] Frerick, L., Extension operators for spaces of infinitely differentiable Whitney functions. Habilitation thesis, 2001.Google Scholar
[5] Goncharov, A., A compact set without Markov's property but with an extension operator for C∞-functions. Studia Math. (1) 119 (1996), 27–35.Google Scholar
[6] Goncharov, A., Perfect sets of finite class without the extension property. Studia Math. (2) 126 (1997), 161–170.Google Scholar
[7] Goncharov, A. and Kocatepe, M., Isomorphic classification of the spaces of Whitney functions. Michigan Math. J. 44 (1997), 555–577.Google Scholar
[8] Goncharov, A. and Kocatepe, M., A continuum of pairwise nonisomorphic spaces of Whitney functions on Cantor-type sets. Linear Topol. Spaces Complex Anal. 3 (1997), 57–64.Google Scholar
[9] Kolmogorov, A. N., On the linear dimension of topological vector spaces. Dokl. Akad. Nauk SSSR 120 (1958), 239–341 (Russian).Google Scholar
[10] Meise, R. and Vogt, D., Introduction to functional analysis. Clarendon Press, Oxford, 1997.Google Scholar
[11] Mityagin, B. S., Approximate dimension and bases in nuclear spaces. Russian Math. Surveys (4) 16 (1961), 59–127 (English translation).Google Scholar
[12] Nevanlinna, R., Analytic Functions. Springer-Verlag, Berlin-New York, 1970.Google Scholar
[13] Pawłucki, W. and Plésniak, W., Extension of C∞ functions from sets with polynomial cusps. Studia Math. 88 (1988), 279–287.Google Scholar
[14] Pełczyński, A., On the approximation of S-spaces by finite dimensional spaces. Bull. Acad. Polon. Sci. 5 (1957), 879–881.Google Scholar
[15] Pomerenke, Ch., Boundary Behavior of Conformal Maps. Springer-Verlag, Berlin-Heidelberg, 1992.Google Scholar
[16] Stein, E. M., Singular integrals and differentiability properties of functions. Princeton Univ. Press, 1970.Google Scholar
[17] Tidten, M., Fortsetzungen von C∞-Funktionen, welche auf einer abgeschlossenen Menge in R definiert sind. Manuscripta Math. 27 (1979), 291–312.Google Scholar
[18] Tidten, M., Kriterien für die Existenz von Ausdehnungoperatoren zu E(K) für kompakte Teilmengen K von R. Arch.Math. 40 (1983), 73–81.Google Scholar
[19] Tidten, M., A geometric characterization for the property (DN) of E(K) for arbitrary compact subsets K of R. Arch.Math. 77 (2001), 247–252.Google Scholar
[20] Tikhomirov, V. M., On n-th diameters of compact sets. Dokl. Akad. Nauk SSSR (4) 130(1960), 734–737.Google Scholar
[21] Vogt, D., Characterisierung der Unterräume von (s). Math. Z. 155 (1977), 109–117.Google Scholar
[22] Vogt, D. and Wagner, M. J., Characterisierung der Quotienträume von s und eine Vermutung von Martineau. Studia Math. 67 (1980), 225–240.Google Scholar
[23] Zahariuta, V. P., Some linear topological invariants and isomorphisms of tensor products of scale's centers. Izv. Severo-Kavkaz. Nauchn. Centra Vyssh. Shkoly 4 (1974), 62–64 (in Russian).Google Scholar