Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-05-12T00:22:11.618Z Has data issue: false hasContentIssue false
  • English
  • Français

Smooth Polynomial Solutions to aTernary Additive Equation

Published online by Cambridge University Press:  20 November 2018

Junsoo Ha
Junsoo Ha*
Affiliation:
Korea Institute for Advanced Study, 85 Hoegiro, Dongdaemungu, Seoul, Republic of Korea e-mail: junsooha@kias.re.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 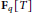${{\mathbf{F}}_{q}}[T]$ be the ring of polynomials over the finite field of $q$ elements and $Y$ a large integer. We say a polynomial in 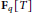${{\mathbf{F}}_{q}}[T]$ is $Y$-smooth if all of its irreducible factors are of degree at most $Y$. We show that a ternary additive equation 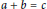$a\,+\,b\,=\,c$ over $Y$-smooth polynomials has many solutions. 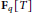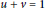As an application, if $S$ is the set of first $s$ primes in ${{\mathbf{F}}_{q}}[T]$ and $s$ is large, we prove that the $S$-unit equation $u\,+\,v\,=\,1$ has at least $\text{exp}\left( {{s}^{1/6-\in }}\,\text{log}\,\text{q} \right)$ solutions.

Keywords

11T5511D0411L0711T23smooth numberpolynomial over a finite fieldcircle method
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 1 , 01 February 2018 , pp. 117 - 141
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Drappeau, Sary, Sur les solutions friables de l'équation a + b = c. Math. Proc. Cambridge Philos. Soc. 154(2013), no. 3, 439–463.http://dx.doi.Org/10.1017/S0305004112000643 Google Scholar
[2] Drappeau, Sary, Théorèmes de type Fouvry-Iwaniec pour les entiers friables. Compos. Math. 151(2015), no. 5, 828–862.http://dx.doi.Org/10.1112/S0010437X14007933 Google Scholar
[3] Erdös, P., Stewart, C. L., and Tijdeman, R., Some Diophantine equations with many solutions. Compositio Math. 66(1988), no. 1, 37–56.Google Scholar
[4] Evertse, J.-H., On equations in S-units and the Thue-Mahler equation. Invent. Math. 75(1984), no. 3, 561–584.http://dx.doi.org/10.1007/BF01388644 Google Scholar
[5] Ha, Junsoo, Some problems in multiplicative number theory. Ph.D. thesis, Stanford University, 2014.Google Scholar
[6] Harper, A. J., On finding many solutions to S-unit equations by solving linear equations on average. arxiv:1108.3819 Google Scholar
[7] Harper, A. J., Bombieri-Vinogradov and Barban-Davenport-Halberstam type theorems for smooth numbers. arxiv:1208.5992 Google Scholar
[8] Harper, A. J., Minor arcs, mean values, and restriction theory for exponential sums over smooth numbers. Compos. Math. 152(2016), no. 6,1121–1158.http://dx.doi.Org/10.1112/S0010437X1 5007782 Google Scholar
[9] Hayes, David R., The distribution of irreducibles in GF[q, x]. Trans. Amer. Math. Soc. 117(1965),101–127.Google Scholar
[10] Hayes, David R., The expression of a polynomial as a sum of three irreducibles. Acta Arith. 11(1966), 461–488.Google Scholar
[11] Hayes, David R., Explicit class field theory for rational function fields. Trans. Amer. Math. Soc. 189(1974), 77–91.http://dx.doi.Org/10.1090/S0002-9947-1 974-0330106-6 Google Scholar
[12] Hsu, Chih-Nung, The distribution of irreducible polynomials in F9 [t]. J. Number Theory 61(1996),no. 1, 85–96. http://dx.doi.org/10.1006/jnth.1996.0139 Google Scholar
[13] Konyagin, S. and Soundararajan, Kannan, Two S-unit equations with many solutions. J. Number Theory 124(2007), no. 1, 193–199.http://dx.doi.Org/10.1016/j.jnt.2006.07.017 Google Scholar
[14] Kubota, R. M., Waring's problem for Fq[x]. Dissertationes Math. (Rozprawy Mat.) 117(1974), 60.Google Scholar
[15] Lagarias, Jeffrey C. and Soundararajan, Kannan, Smooth solutions to the abc equation: the xyz conjecture. J. Théor. Nombres Bordeaux 23(2011), no. 1, 209–234. http://dx.doi.org/10.5802/jtnb.757 Google Scholar
[16] Lagarias, Jeffrey C., Counting smooth solutions to the equation A + B = C. Proc. Lond. Math. Soc. 104(2012), no. 4, 770–798.http://dx.doi.Org/10.1112/plms/pdr037 Google Scholar
[17] Liu, Yu-Ru and Wooley, Trevor D., Waring's problem in function fields. J. Reine Angew. Math. 638(2010), 1–67.http://dx.doi.org/10.1515/crelle.2010.001 Google Scholar
[18] Manstavicius, E., Remarks on elements of semigroups that are free of large prime factors. Liet. Mat. Rink. 32(1992), no. 4, 512–525.Google Scholar
[19] Manstavicius, E., Semigroup elements free of large prime factors. In: New trends in probability and statistics. Vol. 2 (Palanga, 1991), pages 135–153. VSP, Utrecht, 1992.Google Scholar
[20] Ramakrishnan, Dinakar and Valenza, Robert J., Fourier analysis on number fields, Graduate Texts in Mathematics, 186. Springer-Verlag, New York, 1999.Google Scholar
[21] Rosen, Michael, Number theory in function fields. Graduate Texts in Mathematics, 210. Springer-Verlag, New York, 2002.Google Scholar