Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-07T09:36:23.456Z Has data issue: false hasContentIssue false
  • English
  • Français

The smallest Prime Value of xn + a

Published online by Cambridge University Press:  20 November 2018

Kevin S. McCurley
Kevin S. McCurley*
Affiliation:
Michigan State University, East Lansing, Michigan University of Southern California, Los Angeles, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let a and n be positive integers such that f(x) = xn + a is irreducible over the integers. A conjecture made by Bouniakowsky [4] in 1857 would imply that there exist infinitely many integers x such that f(x) is prime. An even stronger conjecture of Bateman and Horn [1, 2] would imply that

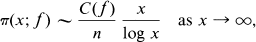
where π(x;f) is the number of integers m with 0 ≧ m ≧ x for which f(m) is prime, and

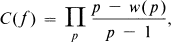
where w(p) is the number of solutions of the congruence

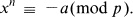
Except for the trivial case n = 1, neither of these conjectures has ever been resolved.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 4 , 01 August 1986 , pp. 925 - 936
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Bateman, P. and Horn, R., A heuristic asymptotic formula concerning the distribution of prime numbers, Math. Comp. 16 (1962), 363–367.Google Scholar
2. Bateman, P. and Horn, R., Primes represented by polynomials in one variable, Proc. Symp. Pure Math. 8 (1965), 119–135.Google Scholar
3. Bombieri, E., Le grand crible dans la théorie analytique des nombres. Avec une sommaire en anglais, Astérisque 18 (Société Mathématiques de France, Paris, 1974).Google Scholar
4. Bouniakowsky, V., Sur les diviseurs numériques invariables des fonctions rationelles entières, Mem. Acad. Sci. St. Petersburg 6 (1857), 305–329.Google Scholar
5. Brillhart, J., Note on irreducibility testing, Math. Comp. 35 (1980), 1379–1381.Google Scholar
6. de Bruijn, N. G., On the number of positive integers ≦ x and free of prime factors > y, Nederl. Akad. Wetensch. Proc. Ser. A 54 (1951), 50–60.Google Scholar
7. LeVeque, W. J., Fundamentals of number theory (Addison-Wesley, Reading, MA, 1977).Google Scholar
8. McCurley, K. S., Prime values of polynomials and irreducibility testing, Bull. Amer. Math. Soc. (N.S.) 77 (1984), 155–158.Google Scholar
9. Norton, K. K., On the number of restricted prime factors of an integer I, Illinois J. Math. 20 (1976), 681–705.Google Scholar
10. Rankin, R. A., The difference between consecutive prime numbers V, Proc. Edinburgh Math. Soc. (2) 13 (1962/63), 331–332.Google Scholar