Hostname: page-component-77c89778f8-n9wrp Total loading time: 0 Render date: 2024-07-17T03:56:02.060Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-Poisson Manifolds

Published online by Cambridge University Press:  20 November 2018

A. Alekseev ,
Y. Kosmann-Schwarzbach  and
E. Meinrenken
A. Alekseev
Affiliation:
Institute for Theoretical Physics Uppsala University Box 803 S-75108 Uppsala Sweden, email: alekseev@teorfys.uu.se
Y. Kosmann-Schwarzbach
Affiliation:
Centre de Mathématiques (U.M.R. du C.N.R.S. 7640) Ecole Polytechnique F-91128 Palaiseau France, email: yks@math.polytechnique.fr
E. Meinrenken
Affiliation:
University of Toronto Department of Mathematics 100 St George Street Toronto, Ontario M5S3G3, email: mein@math.toronto.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A quasi-Poisson manifold is a $G$-manifold equipped with an invariant bivector field whose Schouten bracket is the trivector field generated by the invariant element in 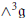${{\Lambda }^{3}}\mathfrak{g}$ associated to an invariant inner product. We introduce the concept of the fusion of such manifolds, and we relate the quasi-Poisson manifolds to the previously introduced quasi-Hamiltonian manifolds with group-valued moment maps.

Keywords

53D
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 1 , 01 February 2002 , pp. 3 - 29
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Alekseev, A. and Kosmann-Schwarzbach, Y., Manin pairs and moment maps. math.DG/9909176, to appear.Google Scholar
[2] Alekseev, A., Malkin, A. and Meinrenken, E., Lie group valued moment maps. J. Differential Geom. 48 (1998), 445–495.Google Scholar
[3] Alekseev, A. and Meinrenken, E., The non-commutative Weil algebra. Invent. Math. 139 (2000), 135–172.Google Scholar
[4] Etingof, P. and Varchenko, A., Geometry and classification of solutions of the classical dynamical Yang-Baxter equation. Comm. Math. Phys. 192 (1998), 77–120.Google Scholar
[5] Fock, V. V. and Rosly, A. A., Poisson structure on moduli of flat connections on Riemann surfaces and the r-matrix. Moscow Seminar in Mathematical Physics, Amer. Math. Soc. Transl. Ser. 2 191 (1999), 67–86.Google Scholar
[6] Goldman, W., The symplectic nature of fundamental groups of surfaces. Adv. in Math. 54 (1984), 200–225.Google Scholar
[7] Semenov-Tian-Shansky, M., Monodromy map and classical r-matrices. Zapiski Nauchn. Semin. POMI (St.Petersburg) 200(1993), hep-th/9402054.Google Scholar
[8] Treloar, T., The symplectic geometry of polygons in the 3-sphere. Canad. J. Math., this issue, 30–54.Google Scholar
[9] Vaisman, I., Lectures on the Geometry of Poisson Manifolds. Birkhäuser, 1994.Google Scholar
[10] Weinstein, A., The modular automorphism group of a Poisson manifold. J. Geom. Phys. 23 (1997), 379–394.Google Scholar