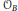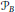Given a Bratteli diagram $B$, we study the set ${{\mathcal{O}}_{B}}$ of all possible orderings on $B$ and its subset ${{\mathcal{P}}_{B}}$ consisting of perfect orderings that produce Bratteli–Vershik topological dynamical systems (Vershik maps). We give necessary and sufficient conditions for the ordering 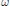$\omega $ to be perfect. On the other hand, a wide class of non-simple Bratteli diagrams that do not admit Vershik maps is explicitly described. In the case of finite rank Bratteli diagrams, we show that the existence of perfect orderings with a prescribed number of extreme paths constrains significantly the values of the entries of the incidence matrices and the structure of the diagram $B$. Our proofs are based on the new notions of skeletons and associated graphs, defined and studied in the paper. 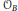For a Bratteli diagram $B$ of rank $k$, we endow the set ${{\mathcal{O}}_{B}}$ with product measure $\mu $ and prove that there is some 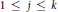$1\,\le \,j\,\le \,k$ such that $\mu $-almost all orderings on $B$ have 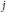$j$ maximal and 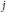$j$ minimal paths. If 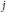$j$ is strictly greater than the number of minimal components that $B$ has, then $\mu $-almost all orderings are imperfect.