Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
Hostname: page-component-78dcdb465f-9pqtr Total loading time: 2.54 Render date: 2021-04-20T05:28:52.682Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false, "newCitedByModal": true }
EnglishFrançais
Canadian Journal of Mathematics Canadian Journal of Mathematics

Article contents

Partial Differential Hamiltonian Systems

Published online by Cambridge University Press:  20 November 2018

Luca Vitagliano
Luca Vitagliano
Affiliation:
DipMat, University of Salerno, and Istituto Nazionale di Fisica Nucleare, GC Salerno, via Ponte don Melillo, 84084 Fisciano (SA) Italy, e-mail: lvitagliano@unisa.it
Corresponding
E-mail address:
lvitagliano@unisa.it
Save pdf (0.45 megabytes)Save pdf (0.45 mb)
Rights & Permissions[Opens in a new window]

Abstract

We define partial differential (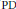 $\text{PD}$ in the following), i.e., field theoretic analogues of Hamiltonian systems on abstract symplectic manifolds and study their main properties, namely, 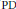$\text{PD}$ Hamilton equations, 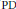$\text{PD}$ Noether theorem, 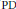$\text{PD}$ Poisson bracket, etc. Unlike the standard multisymplectic approach to Hamiltonian field theory, in our formalism, the geometric structure (kinematics) and the dynamical information on the “phase space” appear as just different components of one single geometric object.

Keywords

70S05 70S10 53C80 field theory fiber bundles multisymplectic geometry Hamiltonian systems
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 5 , 01 October 2013 , pp. 1164 - 1200
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Aldaya, V., and de Azcárraga, J., Higher Order Hamiltonian Formalism in Field Theory. J. Phys. A: Math. Gen. 13(1982), 2545. http://dx.doi.org/10.1088/0305-4470/13/8/004 CrossRefGoogle Scholar
[2] Alonso-Blanco, R. J. and Vinogradov, A. M., Green Formula and Legendre Transformation. Acta Appl. Math. 83(2004), 149. http://dx.doi.org/10.1023/B:ACAP.0000035594.33327.71 CrossRefGoogle Scholar
[3] Awane, A., k-Symplectic Structures. J. Math. Phys. 32(1992), 4046. http://dx.doi.org/10.1063/1.529855 CrossRefGoogle Scholar
[4] Bocharov, A. V., Chetverikov, V. N., Duzhin, S. V., Khor’kova, N. G., Krasil’shchik, I. S., Samokhin, A. V., Torkhov, Yu. N., Verbovetsky, A. M., and Vinogradov, A. M., Symmetries and Conservation Laws for Differential Equations of Mathematical Physics. Transl. Math. Mon. 182, Amer. Math. Soc., Providence, 1999.Google Scholar
[5] Bridges, T. J., Multi-symplectic Structures and Wave Propagation. Math. Proc. Camb. Philos. Soc. 121(1997), 147. http://dx.doi.org/10.1017/S0305004196001429 CrossRefGoogle Scholar
[6] Bridges, T. J. and Reich, S., Multi-symplectic Integrators: Numerical Schemes for Hamiltonian PDEs that Preserve Symplecticity. Phys. Lett. A284(2001), 184. http://dx.doi.org/10.1016/S0375-9601(01)00294-8 CrossRefGoogle Scholar
[7] Cantrijn, F. and Ibort, A.. de Lóen, M., On the Geometry of Multisymplectic Manifolds. J. Austral. Math. Soc. Ser. A 66(1999), 303. http://dx.doi.org/10.1017/S1446788700036636 CrossRefGoogle Scholar
[8] Cotter, C. J., Holm, D. D., and Hydon, P. E., Multisymplectic Formulation of Fluid Dynamics Using the Inverse Map. Proc. Roy. Soc. A463(2007), 2671. chttp://dx.doi.org/10.1098/rspa.2007.1892 CrossRefGoogle Scholar
[9] Crnković, C. and Witten, E., Covariant Description of Canonical Formalism in Geometrical Theories. In: Three Hundred Years of Gravitation (eds. S.W. Hawking andW. Israel), Cambridge University Press, Cambridge, 1987, 676.Google Scholar
[10] Dedecker, P., On the Generalization of Symplectic Geometry to Multiple Integrals in the Calculus of Variations. Lecture Notes in Math. 570, Springer, Berlin, 1977, 395.Google Scholar
[11] de Lecn, M., Marín-Solano, J., and Marrero, J. C., The Constraint Algorithm in the Jet Formalism. Diff. Geom. Appl. 6(1996), 275. http://dx.doi.org/10.1016/0926-2245(96)82423-5 CrossRefGoogle Scholar
[12] de León, M., A Geometrical Approach to Classical Field Theories: a Constraint Algorithm for Singular Theories. Math. Appl. 350, Kluwer, Dordrecht, 1996, 291.Google Scholar
[13] de León, M., Marín-Solano, J., Marrero, J. C., Mu˜ñoz-Lecanda, M. C., and Román-Roy, N., Singular Lagrangian on Jet Bundles. Fort. Phys. 50(2002), 103. arxiv:math-ph/0105012Google Scholar
[14] de León, M., Martin de Diego, D., and Santamaria-Merino, A., Symmetries in Classical Field Theory. Int. J. Geom. Methods Mod. Phys. 1(2004), 651. http://dx.doi.org/10.1142/S0219887804000290 CrossRefGoogle Scholar
[15] de León, M., Marín-Solano, J., Marrero, J. C., Mu˜ñoz-Lecanda, M. C., and Román-Roy, N., Pre-Multisymplectic Constraint Algorithm for Field Theories. Int. J. Geom. Methods Mod. Phys. 2(2005), 839. http://dx.doi.org/10.1142/S0219887805000880 CrossRefGoogle Scholar
[16] Dubrovin, B. A. and Novikov, S. P., Hamiltonian Formalism of One-Dimensional Systems of Hydrodynamic Type and the Bogolyubov–Whitham Averaging Method. Dokl. Akad. Nauk SSSR 270(1983), 781–785; Soviet Math. Dokl. 27(1983), 665.Google Scholar
[17] Dubrovin, B. A., On Poisson Brackets of Hydrodynamic Type. Dokl. Akad. Nauk SSSR 279(1984), 294–297; Soviet Math. Dokl. 30(1984), 651.Google Scholar
[18] Echeverría-Enríquez, A., Mu˜ñoz-Lecanda, M. C., and N. Román-Roy, , Geometry of Multisymplectic Hamiltonian First-Order Field Theories. J. Math. Phys. 41(2000), 7402. http://dx.doi.org/10.1063/1.1308075 CrossRefGoogle Scholar
[19] Echeverría-Enríquez, A., Geometry of Lagrangian First-Order Classical Field Theories. Forts. Phys. 44(1996), 235. http://dx.doi.org/10.1002/prop.2190440304 CrossRefGoogle Scholar
[20] Forger, M. and Gomes, L., Multisymplectic and Polysymplectic Structures on Fiber Bundles. arxiv:0708.1596Google Scholar
[21] Forger, M., Paufler, C., and Römer, H., The Poisson Bracket for Poisson Forms in Multisymplectic Field Theory. Rev. Math. Phys. 15(2003), 705. http://dx.doi.org/10.1142/S0129055X03001734 CrossRefGoogle Scholar
[22] Forger, M., A General Construction of Poisson Brackets on Exact Multisymplectic Manifolds. Rep. Math. Phys. 51(2003), 187. http://dx.doi.org/10.1016/S0034-4877(03)80012-5 CrossRefGoogle Scholar
[23] Forger, M., Hamiltonian Multivector Fields and Poisson Forms in Multisymplectic Field Theory. J. Math. Phys. 46(2005), 112903. http://dx.doi.org/10.1063/1.2116320 CrossRefGoogle Scholar
[24] Forger, M. and Römer, H., A Poisson Bracket on Multisymplectic Phase Space. Rep. Math. Phys. 48(2001), 211. http://dx.doi.org/10.1016/S0034-4877(01)80081-1 CrossRefGoogle Scholar
[25] Forger, M. and Romero, S., Covariant Poisson Brackets in Geometric Field Theory. Commun. Math. Phys. 256(2005), 375. http://dx.doi.org/10.1007/s00220-005-1287-8 CrossRefGoogle Scholar
[26] Goldshmidt, H. and Sternberg, S., The Hamilton–Cartan Formalism in the Calculus of Variations. Ann. Inst. Fourier 23(1973), 203. http://dx.doi.org/10.5802/aif.451 CrossRefGoogle Scholar
[27] Gotay, M. J., A Multisymplectic Approach to the KdV Equation. In: Differential Geometric Methods in Mathematical Physics (eds. K. Bleuler and M.Werner), Kluwer, Amsterdam, 1988, 295.Google Scholar
[28] Gotay, M. J., Isenberg, J., and Marsden, J. E., Momentum Maps and Classical Relativistic Fields. I: Covariant Field Theory. arxiv:physics/9801019Google Scholar
[29] Gotay, M. J., Nester, J. M., and Hinds, G., Presymplectic Manifolds and the Dirac–Bergmann Theory of Constraints. J. Math. Phys. 19(1978), 2388. http://dx.doi.org/10.1063/1.523597 CrossRefGoogle Scholar
[30] Grabowska, K., A Tulczyjew Triple for Classical Fields. J. Phys. A: Math. Theor. 45(2012), 145207. http://dx.doi.org/10.1088/1751-8113/45/14/145207 CrossRefGoogle Scholar
[31] Grabowska, K., Grabowski, J., and Urbański, P., AV-Differential Geometry: Poisson and Jacobi Structures. J. Geom. Phys. 52(2004), 398. http://dx.doi.org/10.1016/j.geomphys.2004.04.004 CrossRefGoogle Scholar
[32] Grabowska, K., AV-Differential Geometry: Euler–Lagrange Equations. J. Geom. Phys. 57(2007), 1984. http://dx.doi.org/10.1016/j.geomphys.2007.04.003 CrossRefGoogle Scholar
[33] Gracia, X., Martin, R., and Román-Roy, N., Constraint Algorithm for k-Presymplectic Hamiltonian Systems. Application to Singular Field Theories. Int. J. Geom. Methods Mod. Phys. 6(2009), 851. http://dx.doi.org/10.1142/S0219887809003795 CrossRefGoogle Scholar
[34] Hélein, F. and Kouneiher, J., Covariant Hamiltonian Formalism for the Calculus of Variations with Several Variables: Lepage–Dedecker versus De Donder–Weyl. Adv. Theor. Math. Phys. 8(2004), 565.CrossRefGoogle Scholar
[35] Henneaux, M. and Teitelboim, C., Quantization of Gauge Systems. Princeton University Press, Princeton, 1992.Google Scholar
[36] Kanatchikov, I. V., On Field Theoretic Generalization of a Poisson Algebra. Rep. Math. Phys. 40(1997), 225. http://dx.doi.org/10.1016/S0034-4877(97)85919-8 CrossRefGoogle Scholar
[37] Kijowski, J., A Finite-Dimensional Canonical Formalism in the Classical Field Theory. Commun. Math. Phys. 30(1973), 99. http://dx.doi.org/10.1007/BF01645975 CrossRefGoogle Scholar
[38] Kijowski, J. and Szczyrba, W., Multisymplectic Manifolds and the Geometrical Construction of the Poisson Bracket in Field Theory. In: Géométrie Symplectique et Physique Mathématique (ed. J.-M. Souriau), Colloq. Internat. C. N. R. S. 237(1975), 347.Google Scholar
[39] Kolář, I., A Geometric Version of the Higher Order Hamilton Formalism in Fibered Manifolds. J. Geom. Phys. 1(1984), 127. http://dx.doi.org/10.1016/0393-0440(84)90007-X CrossRefGoogle Scholar
[40] Krupkova, O., Hamiltonian Field Theory. J. Geom. Phys. 43(2002), 93. http://dx.doi.org/10.1016/S0393-0440(01)00087-0 CrossRefGoogle Scholar
[41] Lee, J. and Wald, R., Local Symmetries and Constraints. J. Math. Phys. 31(1990), 725. http://dx.doi.org/10.1063/1.528801CrossRefGoogle Scholar
[42] Marsden, J., Pekarsky, S., Shkoller, S., and West, M., Variational Methods, Multisymplectic Geometry and Continuum Mechanics. J. Geom. Phys. 38(2001), 253. http://dx.doi.org/10.1016/S0393-0440(00)00066-8 CrossRefGoogle Scholar
[43] Martin, G., A Darboux Theorem for Multisymplectic Manifolds. Lett. Math. Phys. 16(1988), 133.http://dx.doi.org/10.1007/BF00402020 CrossRefGoogle Scholar
[44] Michor, P.W., Topics in Differential Geometry. Graduate Stud. in Math. 93, Amer. Math. Soc., Providence, 2008.Google Scholar
[45] Mokhov, O. I., Symplectic and Poisson Geometry on Loop Spaces of Manifolds and Nonlinear Equations. Uspekhi Mat. Nauk 53(1998), 85–192; (English) Russian Math. Surveys 53(1998), 515.http://dx.doi.org/10.4213/rm19 Google Scholar
[46] Moreno, G., Vinogradov, A. M., and Vitagliano, G., Integrals and Cohomology. In preparation.Google Scholar
[47] Paufler, C. and Römer, H., Geometry of Hamiltonian n-Vectors in Multisymplectic Field Theory. J. Geom. Phys. 44(2002), 52. http://dx.doi.org/10.1016/S0393-0440(02)00031-1 CrossRefGoogle Scholar
[48] Paufler, C., de Donder–Weyl Equations and Multisymplectic Geometry. Rep. Math. Phys. 49(2002), 325. http://dx.doi.org/10.1016/S0034-4877(02)80030-1 CrossRefGoogle Scholar
[49] Román-Roy, N., Multisymplectic Lagrangian and Hamiltonian Formalism of First-Order Classical Field Theories. SIGMA 5(2009), 100.arxiv:math-ph/0506022Google Scholar
[50] Saunders, D. J., Jet Fields, Connections and Second-Order Differential Equations. J. Phys. A: Math. Gen. 20(1987), 3261.http://dx.doi.org/10.1088/0305-4470/20/11/029 CrossRefGoogle Scholar
[51] Saunders, D. J., The Geometry of Jet Bundles. Cambridge University Press, Cambridge, 1989.Google Scholar
[52] Saunders, D. J., A Note on Legendre Transformations. Diff. Geom. Appl. 1(1991), 109. http://dx.doi.org/10.1016/0926-2245(91)90025-5CrossRefGoogle Scholar
[53] Saunders, D. J. and Crampin, M., On the Legendre Map in Higher-Order Field Theories. J. Phys. A: Math. Gen. 23(1990), 3169. http://dx.doi.org/10.1088/0305-4470/23/14/016 CrossRefGoogle Scholar
[54] Shadwick, W. F., The Hamiltonian Formulation of Regular r-th Order Lagrangian Field Theories. Lett. Math. Phys. 6(1982), 409.http://dx.doi.org/10.1007/BF00405859 CrossRefGoogle Scholar
[55] Vinogradov, A. M., The –Spectral Sequence, Lagrangian Formalism and Conservation Laws I, II. J. Math. Anal. Appl. 100(1984), 1.http://dx.doi.org/10.1016/0022-247X(84)90071-4 Google Scholar
[56] Vitagliano, L., Secondary Calculus and the Covariant Phase Space. J. Geom. Phys. 59(2009), 426.http://dx.doi.org/10.1016/j.geomphys.2008.12.001 CrossRefGoogle Scholar
[57] Vitagliano, L., The Lagrangian–Hamiltonian Formalism for Higher Order Field Theories. J. Geom. Phys. 60(2010), 857.http://dx.doi.org/10.1016/j.geomphys.2010.02.003 CrossRefGoogle Scholar
[58] Zuckerman, G. J., Action Principles and Global Geometry. In: Mathematical Aspects of String Theory (ed. S. T. Yau),World Scientific, Singapore, 1987, 259.CrossRefGoogle Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 43 *
View data table for this chart

* Views captured on Cambridge Core between 20th November 2018 - 20th April 2021. This data will be updated every 24 hours.

You have Access
3
Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Partial Differential Hamiltonian Systems
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

Partial Differential Hamiltonian Systems
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

Partial Differential Hamiltonian Systems
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *