Article contents
On Some Explicit Constructions of Finsler Metrics with Scalar Flag Curvature
Published online by Cambridge University Press: 20 November 2018
Abstract
We give an explicit construction of polynomial (of arbitrary degree) 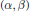 $(\alpha ,\,\beta )$-metrics with scalar flag curvature and determine their scalar flag curvature. These Finsler metrics contain all nontrivial projectively flat
$(\alpha ,\,\beta )$-metrics with scalar flag curvature and determine their scalar flag curvature. These Finsler metrics contain all nontrivial projectively flat 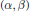 $(\alpha ,\,\beta )$-metrics of constant flag curvature.
$(\alpha ,\,\beta )$-metrics of constant flag curvature.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010
Footnotes
This work is supported by the National Natural Science Foundation of China 10471001.
References
- 6
- Cited by




