Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-26T06:25:25.760Z Has data issue: false hasContentIssue false
  • English
  • Français

On pointwise a.e. convergence of multilinear operators

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  29 May 2023

Loukas Grafakos ,
Danqing He ,
Petr Honzík Open the ORCID record for Petr Honzík [Opens in a new window]  and
Bae Jun Park
Loukas Grafakos
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MO 65211, USA e-mail: grafakosl@umsystem.edu
Danqing He
Affiliation:
School of Mathematical Sciences, Fudan University, Shanghai, People’s Republic of China e-mail: hedanqing@fudan.edu.cn
Petr Honzík
Affiliation:
Department of Mathematics, Charles University, 116 36 Praha 1, Czech Republic e-mail: honzik@gmail.com
Bae Jun Park*
Affiliation:
Department of Mathematics, Sungkyunkwan University, Suwon 16419, Republic of Korea
*
e-mail: bpark43@skku.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, we obtain the pointwise almost everywhere convergence for two families of multilinear operators: (a) the doubly truncated homogeneous singular integral operators associated with 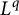$L^q$ functions on the sphere and (b) lacunary multiplier operators of limited smoothness. The a.e. convergence is deduced from the 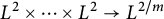$L^2\times \cdots \times L^2\to L^{2/m}$ boundedness of the associated maximal multilinear operators.

Keywords

Multilinear operatorsrough singular integral operatorlacunary maximal multiplier

MSC classification

Primary: 42B15: Multipliers
Secondary: 42B25: Maximal functions, Littlewood-Paley theory
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 28
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

D. He is supported by the National Key R&D Program of China (Grant No. 2021YFA1002500), the NNSF of China (Grant Nos. 11701583 and 12161141014), and the Natural Science Foundation of Shanghai (Grant No. 22ZR1404900). L. Grafakos would like to acknowledge the support of the Simons Fellows program (Grant No. 819503) and of the Simons Foundation grant 624733. P. Honzík is supported by the grant GAČR P201/21-01976S. B. Park is supported by the NRF grant 2022R1F1A1063637.

References

Anderson, T. and Palsson, E., Bounds for discrete multilinear spherical maximal functions . Collect. Math. 73(2022), no. 1, 75–87.CrossRefGoogle Scholar
Barrionuevo, J., Grafakos, L., He, D., Honzík, P., and Oliveira, L., Bilinear spherical maximal function . Math. Res. Lett. 25(2018), no. 5, 1369–1388.CrossRefGoogle Scholar
Buriánková, E. and Honzík, P., Rough maximal bilinear singular integrals . Collect. Math. 70(2019), 431–446.CrossRefGoogle Scholar
Calderón, C., Lacunary spherical means . Ill. J. Math. 23(1979), no. 3, 476–484.Google Scholar
Carbery, A., Rubio de Francia, J., and Vega, L., Almost everywhere summability of Fourier integrals . J. Lond. Math. Soc. 38(1988), no. 3, 513–524.CrossRefGoogle Scholar
Carleson, L., On convergence and growth of partial sums of Fourier series . Acta Math. 116(1966), 135–157.CrossRefGoogle Scholar
Coifman, R. R. and Weiss, G., Book review: Littlewood–Paley and multiplier theory . Bull. Amer. Math. Soc. 84(1978), no. 2, 242–250.CrossRefGoogle Scholar
Coifman, R. R. and Meyer, Y., On commutators of singular integrals and bilinear singular integrals . Trans. Amer. Math. Soc. 212(1975), 315–331.CrossRefGoogle Scholar
Coifman, R. R. and Meyer, Y., Commutateurs d’ intégrales singulières et opérateurs multilinéaires . Ann. Inst. Fourier (Grenoble) 28(1978), 177–202.CrossRefGoogle Scholar
Dosidis, G., Multilinear spherical maximal function . Proc. Amer. Math. Soc. 149(2021), no. 4, 1471–1480.CrossRefGoogle Scholar
Dosidis, G. and Grafakos, L., On families between the Hardy–Littlewood and spherical maximal functions . Ark. Mat. 59(2021), no. 2, 323–343.CrossRefGoogle Scholar
Du, X., Guth, L., and Li, X., A sharp Schrödinger maximal estimate in ${\mathbb{R}}^2$ . Ann. of Math. 186(2017), no. 2, 607–640.CrossRefGoogle Scholar
Duoandikoetxea, J. and Rubio de Francia, J.-L., Maximal and singular integral operators via Fourier transform estimates . Invent. Math. 84(1986), 541–561.CrossRefGoogle Scholar
Grafakos, L., Classical Fourier analysis. 3rd ed., Graduate Texts in Mathematics, 249, Springer, New York, 2014.CrossRefGoogle Scholar
Grafakos, L., Modern Fourier analysis. 3rd ed., Graduate Texts in Mathematics, 250, Springer, New York, 2014.CrossRefGoogle Scholar
Grafakos, L., He, D., and Honzík, P., Rough bilinear singular integrals . Adv. Math. 326(2018), 54–78.CrossRefGoogle Scholar
Grafakos, L., He, D., and Honzík, P., Maximal operators associated with bilinear multipliers of limited decay . J. Anal. Math. 143(2021), 231–251.CrossRefGoogle Scholar
Grafakos, L., He, D., Honzík, P., and Park, B., Initial ${L}^2\times \cdots \times {L}^2$ bounds for multilinear operators . Trans. Amer. Math. Soc. 376(2023), 3445–3472.CrossRefGoogle Scholar
Grafakos, L., He, D., and Slavíková, L., ${L}^2\times {L}^2\to {L}^1$ boundedness criteria . Math. Ann. 376(2020), 431–455.CrossRefGoogle Scholar
Grafakos, L. and Torres, R. H., Maximal operator and weighted norm inequalities for multilinear singular integrals . Indiana Univ. Math. J. 51(2002), 1261–1276.CrossRefGoogle Scholar
Grafakos, L. and Torres, R. H., Multilinear Calderón–Zygmund theory . Adv. Math. 165(2002), 124–164.CrossRefGoogle Scholar
Heo, Y., Hong, S., and Yang, C., Improved bounds for the bilinear spherical maximal operators . Math. Res. Lett. 27(2020), no. 2, 397–434.CrossRefGoogle Scholar
Jeong, E. and Lee, S., Maximal estimates for the bilinear spherical averages and the bilinear Bochner–Riesz operators . J. Funct. Anal. 279(2020), no. 7, Article no. 108629, 29 pp.CrossRefGoogle Scholar
Jessen, B., Marcinkiewicz, J., and Zygmund, A., Note on the differentiability of multiple integrals . Fundam. Math. 25(1935), no. 1, 217–234.CrossRefGoogle Scholar
Kato, T., Miyachi, A., and Tomita, N., Boundedness of bilinear pseudo-differential operators of ${S}_{0,0}$ -type on ${L}^2\times {L}^2$ . J. Pseudo-Differ. Oper. Appl. 12(2021), Article no. 15, 38 pp.CrossRefGoogle Scholar
Rubio de Francia, J. L., Maximal functions and Fourier transforms . Duke Math. J. 53(1986), 395–404.CrossRefGoogle Scholar
Stein, E., On limits of sequences of operators . Ann. of Math. 74(1961), no. 2, 140–170.CrossRefGoogle Scholar
Triebel, H., Theory of function spaces, Birkhäuser, Basel–Boston–Stuttgart, 1983.CrossRefGoogle Scholar
Triebel, H., Theory of function spaces. III, Birkhäuser, Basel–Boston–Stuttgart, 2006.Google Scholar
Triebel, H., Bases in function spaces, sampling, discrepancy, numerical integration, EMS Tracts in Mathematics, 11, European Mathematical Society, Zürich, 2010.CrossRefGoogle Scholar
Yamazaki, M., A quasi-homogeneous version of paradifferential operators, I. Boundedness on spaces of Besov type . J. Fac. Sci. Univ. Tokyo Sect. IA Math. 33(1986), 131–174.Google Scholar