Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-25T04:14:40.628Z Has data issue: false hasContentIssue false
  • English
  • Français

On Nilpotent Products of Cyclic Groups—Reexamined by the Commutator Calculus

Published online by Cambridge University Press:  20 November 2018

Hermann V. Waldinger  and
Anthony M. Gaglione
Hermann V. Waldinger
Affiliation:
Polytechnic Institute of New York, Brooklyn, New York
Anthony M. Gaglione
Affiliation:
City College of the City University of New York, New York, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Ruth R. Struik investigated the nilpotent group 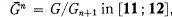, where G is a free product of a finite number of cyclic groups, not all of which are of infinite order, and Gm is the mth subgroup of the lower central series of G. Making use of the “collection process” first given by Philip Hall in [8], she determined 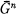completely for 1 ≦ n ≦ p + 1, where p is the smallest prime with the property that it divides the order of at least one of the free factors of G. However, she was unable to proceed beyond n = p + 1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 6 , 01 December 1975 , pp. 1185 - 1210
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Baumslag, Gilbert, Lecture notes on nilpotent groups (American Mathematical Society, Providence, R.I., 1971).Google Scholar
2. Dark, Rex S., On nilpotent products of groups of finite order, Ph.D. Thesis, Cambridge University, England, 1969.Google Scholar
3. Gaglione, Anthony M., Factor groups of the lower central series for special free products, J. Algebra, 37 (1975), 172–185.Google Scholar
4. Gaglione, Anthony M., On free products of finitely generated abelian groups, Trans. Amer. Math. Soc. 195 (1974), 421–430.Google Scholar
5. Gruenberg, K. W., Residual properties of infinite soluble groups, Proc. London Math. Soc. 7 (1957), 29–62.Google Scholar
6. Hall, Marshall Jr., A basis for free lie rings and higher commutators in free groups, Proc. Amer. Math. Soc. 1 (1950), 575–581.Google Scholar
7. Hall, Marshall, The theory of groups (Macmillan, New York, 1959).Google Scholar
8. Hall, Philip, A contribution to the theory of groups of prime power order, Proc. London Math. Soc. 36 (1934), 29–95.Google Scholar
9. Magnus, Wilhelm, Ûber Beziehungen zwischen hbheren Kommutatoren, J. Reine Angew. Math. 177 (1937), 105–115.Google Scholar
10. Magnus, Wilhelm, Abraham Karass and Donald Solitar, Combinatorial Group Theory (Pure and Applied Mathematics 13, Interscience, New York, 1966).Google Scholar
11. Struik, Ruth R., On nilpotent products of cyclic groups, Can. J. Math. 12 (1960), 447–462.Google Scholar
12. Struik, Ruth R., On nilpotent products of cyclic groups II, Can. J. Math. 13 (1961), 557–568.Google Scholar
13. Van der Waerden, B. L., Algebra (7th edition) (Springer-Verlag, Berlin, 1966).Google Scholar
14. Waldinger, Hermann V., A natural linear ordering of basic commutators, Proc. Amer. Math. Soc. 12 (1961), 140–147.Google Scholar
15. Waldinger, Hermann V., Addendum to The lower central series of groups of a special class, J. Algebra 25 (1973), 172–175.Google Scholar
16. Waldinger, Hermann V., On extending Witt's formula, J. Algebra 5 (1967), 41–58.Google Scholar
17. Waldinger, Hermann V., The lower central series of groups of a special class, J. Algebra 14 (1970), 229–244.Google Scholar
18. Waldinger, Hermann V., Two theorems in the commutator calculus, Trans. Amer. Math. Soc. 167 (1972), 384–397.Google Scholar
19. Witt, Ernst, Treue Darstellung Liescher Ringe, J. Reine Angew. Math. 177 (1937), 152–160.Google Scholar