Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-26T01:11:04.624Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Family of Distributions obtained from Orbits

Published online by Cambridge University Press:  20 November 2018

James Arthur
James Arthur*
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that G is a reductive algebraic group defined over a number field F. The trace formula is an identity

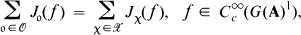
of distributions. The terms on the right are parametrized by “cuspidal automorphic data”, and are defined in terms of Eisenstein series. They have been evaluated rather explicitly in [3]. The terms on the left are parametrized by semisimple conjugacy classes and are defined in terms of related G(A) orbits. The object of this paper is to evaluate these terms.

In previous papers we have already evaluated 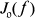in two special cases. The easiest case occurs when corresponds to a regular semisimple conjugacy class 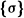in G(F). We showed in Section 8 of [1] that for such an , 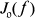could be expressed as a weighted orbital integral over the conjugacy class of σ. (We actually assumed that was “unramified”, which is slightly more general.) The most difficult case is the opposite extreme, in which corresponds to {1}.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 1 , 01 February 1986 , pp. 179 - 214
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Arthur, J., A trace formula for reductive groups I: terms associated to classes in G(Q), Duke Math. J. 45 (1978), 911–952.Google Scholar
2. Arthur, J., The trace formula in invariant form, Ann. of Math. 114 (1981), 1–74.Google Scholar
3. Arthur, J., On a family of distributions obtained from Eisenstein series II: Explicit formulas, Amer. J. Math. 704 (1982), 1289–1336.Google Scholar
4. Arthur, J., The local behaviour of weighted orbital integrals, in preparation.Google Scholar
5. Arthur, J., A measure on the unipotent variety, Can. J. Math. 37 (1985).Google Scholar
6. Clozel, L., Labesse, J. P. and Langlands, R. P., Morning seminar on the trace formula, Lecture Notes, Institute for Advanced Study.Google Scholar
7. Flicker, Y., The trace formula and base change for GL(3), Springer Lecture Notes 927 (1982).CrossRefGoogle Scholar
8. Harish-Chandra, , Harmonic analysis on reductive p-adic groups, Lecture Notes in Math. 162 (Springer-Verlag, Berlin, 1970).CrossRefGoogle Scholar
9. Jacquet, H. and Langlands, R. P., Automorphic forms on GL(2), Springer Lecture Notes 114 (1970).CrossRefGoogle Scholar