Hostname: page-component-848d4c4894-8kt4b Total loading time: 0 Render date: 2024-06-15T22:51:20.575Z Has data issue: false hasContentIssue false
  • English
  • Français

New Almost Periodic Type Functions and Solutions of Differential Equations

Published online by Cambridge University Press:  20 November 2018

Bolis Basit  and
Chuanyi Zhang
Bolis Basit
Affiliation:
Department of Math., Monash University, Clayton, Victoria 3168, Australia e-mail: bbasit@vaxc.cc.monash.edu.au
Chuanyi Zhang
Affiliation:
Department of Math., Harbin Institute of Technology, Harbin, China, 150001
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

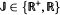Let X be a Banach space and . Let Π and Π0 be two subspaces of , the Banach space of bounded continuous functions from 𝕁 to X. We seek conditions under which Π + Π0 is closed in 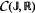. This led to introduce a general 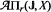space, which contains many classes of almost periodic type functions as subspaces. We prove some recent results on indefinite integral for the elements of these classes. We apply certain results on harmonic analysis to investigate solutions of differential equations. As an application we study specific spaces: the spaces of asymptotic and pseudo almost automorphic functions and their solutions of some ordinary quasi-linear and a non-linear parabolic partial differential equations.

Keywords

43A6028B0543A4534A1235K55Recurrentpseudo almost automorphicasymptotically almost automorphicindefinite integralspectrumparabolic partial equation
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 48 , Issue 6 , 01 December 1996 , pp. 1138 - 1153
Copyright
Copyright © Canadian Mathematical Society 1996

References

1. Amerio, L. and Prouse, G., Almost-periodic Functions and Functional Equations, Van Nostrand, New York, 1971.Google Scholar
2. Basit, B., Some problems concerning different types of vector valued almost periodic functions, Dissertationes Math. 338(1995).Google Scholar
3. Basit, B. and Pryde, A. J., Polynomials and functions with finite spectra on locally compact Abelian groups, Bull. Austral. Math. Soc. 51(1995), 33–42.Google Scholar
4. Basit, B., Harmonic analysis and asymptotic behavior of solutions to the abstract Cauchy problem, Monash Univ. Analysis Paper 91(1994).Google Scholar
5. Basit, B., Spectral characterization of abstract functions, Analele stiintificale univ. “Ai.I. Cuza” din Iasi 28(1982), 25–34.Google Scholar
6. Basit, B., Lesfonctions abstraites presque automorphiques etpresques almost periodiques au sens de Levitan et leurs differences, Bull. Sci. Math. (2)101(1977), 131–148.Google Scholar
7. Basit, B., Note on a theorem ofLevitanfor the integral of almost periodic functions, Rend. 1st. Mathem. Univ. Trieste 5(1973), 9–14.Google Scholar
8. Baskakov, G., Spectral criteria for almost periodicity of solution of functional equations, Math. Notes of Acad, of Sci. USSR. 24(1978), 606–612.Google Scholar
9. Berglund, J. F., Junghenn, H. D. and Milnes, P., Analysis on Semigroups: Function Spaces, Compactifications, Representations, Wiley, Now York, 1989.Google Scholar
10. Bochner, S., A new approach to almost periodicity, Proc. Nat. Acad. Sci. U.S.A. 48(1962), 2039–2043.Google Scholar
11. Corduneanu, C., Almost Periodic Functions, Wiley, New York, 1968.Google Scholar
12. Dunford, N. and Schwartz, J. T., Linear Operators,II, Interscience, New York, 1963.Google Scholar
13. Eberlein, W. F., Abstract ergodic theorems and weak almost periodic functions, Trans. Amer. Math. Soc. 67(1949), 217–240.Google Scholar
14. Flor, P., Rhytmische abbildung abelescher gruppen II Z. Wahrscheinlichkeitstheorie verw Geb. 7(1967), 17–28.Google Scholar
15. Goldberg, S. and Irwin, P., Weakly almost periodic vector valued functions, Dissertationes Math. 157(1979).Google Scholar
16. Levitan, B. M., Integration of almost periodic function with values in Banach spaces, Izv. Akad. Nauk. 30(1966), 1101–1110.Google Scholar
17. Levitan, B. M. and Zhikov, V. V., Almost Periodic Functions and Differential Equations, Cambridge University Press, Cambridge, 1982.Google Scholar
18. Lust, F., Elements ergodiques et totalement ergodiques dans L°°(r), Studia Math. 69(1981), 191–225.Google Scholar
19. Milnes, P., Almost automorphic functions and totally bounded groups, Rocky Mount. J. Math. 7(1977), 231–250.Google Scholar
20. Phong, V. Q., Almost periodic solutions ofVoltera equations, Differential and Integral Equations 7(1994), 1083–1093.Google Scholar
21. Reiter, H., Classical Harmonic Analysis and Locally Compact Groups, Oxford University Press, Oxford, 1968.Google Scholar
22. Ruess, W. M. and Summers, W. H., Ergodic theorems for semigroups of operators, Proc. Amer. Math. Soc. 114(1992), 423–432.Google Scholar
23. Ruess, W. M. and Phóng, V. Q., Asymptotically almost periodic solutions of evolution equations in Banach spaces, J. Differential Equations, to appear.Google Scholar
24. Veech, W. A., Almost automorphic functions on groups, Amer. J. Math. 87(1965), 719–751.Google Scholar
25. Zaidman, S., Almost Periodic Functions in Abstract Spaces, Pitman, Boston, London, Melbourne, 1985.Google Scholar
26. Zhang, C., Pseudo almost periodic solutions of some differential equations, J. Math. Anal. Appl. 181(1994), 62–76.Google Scholar
27. Zhang, C., Integration of vector-valued pseudo almost periodic functions, Proc. Amer. Math. Soc. 121(1994), 167–174.Google Scholar
28. Zhang, C., Vector-valued pseudo almost periodic functions, Czech. Math. J., to appear.Google Scholar