Hostname: page-component-77c89778f8-fv566 Total loading time: 0 Render date: 2024-07-18T09:10:14.092Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Transformations on Matrices: The Invariance of a Class of General Matrix Functions

Published online by Cambridge University Press:  20 November 2018

E. P. Botta
E. P. Botta*
Affiliation:
University of Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Mm(F) be the vector space of m-square matrices

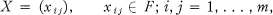
where F is a field; let f be a function on Mm(F) to some set R. It is of interest to determine the linear maps T: Mm(F) → Mm(F) which preserve the values of the function ƒ; i.e., ƒ(T(X)) = ƒ(X) for all X. For example, if we take ƒ(X) to be the rank of X, we are asking for a determination of the types of linear operations on matrices that preserve rank. Other classical invariants that may be taken for f are the determinant, the set of eigenvalues, and the rth elementary symmetric function of the eigenvalues. Dieudonné (1), Hua (2), Jacobs (3), Marcus (4, 6, 8), Mori ta (9), and Moyls (6) have conducted extensive research in this area. A class of matrix functions that have recently aroused considerable interest (4; 7) is the generalized matrix functions in the sense of I. Schur (10).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 281 - 290
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Dieudonné, J., Sur une généralisation du groupe orthogonal à quatre variables, Arch. Math., I (1948), 282–287.Google Scholar
2. Hua, L. K., Geometries of matrices, I. Generalizations of von Staudts’ theorem, Trans. Amer. Math Soc., 57 (1945), 441–481.Google Scholar
3. Jacobs, H. G., Coherence invariant mappings on Kronecker products, Amer. J. Math., 77 (1955), 177–189.Google Scholar
4. Marcus, M., Linear operations on matrices, Amer. Math. Monthly, 69 (1962), 837–847.Google Scholar
5. Marcus, M. and May, F., The permanent function, Can. J. Math., 14 (1962), 177–189.Google Scholar
6. Marcus, M. and Moyls, B. N., Linear transformations on algebras of matrices, Can. J. Math., II (1959) 61–66.Google Scholar
7. Marcus, M. and Mine, H., Inequalities for general matrix functions, Bull. Amer. Math. Soc., 70 (1960) 308–313.Google Scholar
8. Marcus, M. and Purves, R., Linear transformations on algebras of matrices: The invariance of the elementary symmetric functions, Can. J. Math., 11 (1959) 383–396.Google Scholar
9. Morita, K., Schwarz's lemma in a homogeneous space of higher dimensions, Japan J. Math., 19 (1944), 45–56.Google Scholar
10. Schur, I., Über endliche Gruppen und Hermitesche Formen, Math. Z., 1 (1918), 184–207.Google Scholar
11. Weyl, H., The classical groups (Princeton, N.J., 1946).Google Scholar