Article contents
Lattice Octahedra
Published online by Cambridge University Press: 20 November 2018
Extract
Let Ai, A2, … , An be n linearly independent points in n-dimensional Euclidean space of a lattice Λ. The points ± A1, ±A2, . . , ±An define a closed n-dimensional octahedron (or “cross poly tope“) K with centre at the origin O. Our problem is to find a basis for the lattices Λ which have no points in K except ±A1, ±A2, … , ±An.
Let the position of a point P in space be defined vectorially by
1
where the p are real numbers. We have the following results.
When n = 2, it is well known that a basis is
2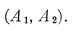
When n = 3, Minkowski (1) proved that there are two types of lattices, with respective bases
3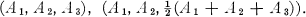
When n = 4, there are six essentially different bases typified by A1, A2, A3 and one of
4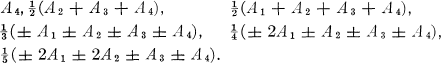
In all expressions of this kind, the signs are independent of each other and of any other signs. This result is a restatement of a result by Brunngraber (2) and a proof is given by Wolff (3).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1960
References
- 8
- Cited by




