Hostname: page-component-77c89778f8-vsgnj Total loading time: 0 Render date: 2024-07-17T12:51:05.634Z Has data issue: false hasContentIssue false
  • English
  • Français

Isometries of sp(α)

Published online by Cambridge University Press:  20 November 2018

R. J. Fleming  and
J. E. Jamison
R. J. Fleming
Affiliation:
Memphis State University, Memphis, Tennessee
J. E. Jamison
Affiliation:
Memphis State University, Memphis, Tennessee
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let l < p < ∞, p ≠ 2 and α > 0. In what follows sp(α) will denote the space of all real or complex sequences for which

(1.1)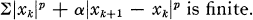

In this paper we show that the spaces sp(α) are Banach spaces under the natural norm and in fact share many properties that the usual lp spaces have. Our main results give characterizations of the surjective isometries of sp(α). These turn out to be quite different than the results for lp. For example, we show that for α ≠ 1, an operator T is a surjective isometry if and only if T is a modulus one multiple of the identity. The methods used are valid for both real and complex scalars. They involve the use of a disjoint support condition together with a property of semi inner products. In the complex case the information on isometries allows us to give complete descriptions of the Hermitian operators as well as the adjoint abelian operators.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 1 , 01 February 1981 , pp. 59 - 67
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Bonsall, F. F. and Duncan, J., Numerical ranges, II, London Mathematical Society Lecture notes 10 (Cambridge University Press, 1973).Google Scholar
2. Fleming, R. J. and Jamison, J. E., Adjoint abelian operators on Lp and C(k), Trans. A.M.S. 217 (1976).Google Scholar
3. Hewitt, E. and Stromberg, K., Real and abstract analysis (Springer Verlag, New York, 1965).Google Scholar
4. Holmes, R. B., Course on optimization and best approximation, Springer Lecture notes 257 (1972).Google Scholar
5. Koehler, D. and Rosenthal, P., On isometries of normed linear spaces, Studia Math. 36 (1970), 213–216.Google Scholar
6. Lamperti, J., On the isometries of certain function-spaces, Pacific J. Math. 2 (1958), 459–566.Google Scholar
7. Lumer, G., Semi inner product spaces, Trans. A.M.S. 100 (1961), 26–43.Google Scholar
8. Palmer, T. W., Unbounded normal operators on Banach spaces, Trans. A.M.S. 133 (1968), 385–414.Google Scholar
9. Stampfli, J. G., Adjoint abelian operators on Banach spaces, Can. J. Math. 21 (1969), 505–512.Google Scholar