Hostname: page-component-77c89778f8-vpsfw Total loading time: 0 Render date: 2024-07-22T23:16:24.585Z Has data issue: false hasContentIssue false
  • English
  • Français

Intrinsic Functions on Semi-Simple Algebras

Published online by Cambridge University Press:  20 November 2018

C. A. Hall
C. A. Hall*
Affiliation:
Data Analysis Directorate, White Sands Missile Range, New Mexico
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Rinehart (5) has introduced and motivated the study of the class of intrinsic functions on a linear associative algebra 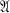, with identity, over the real field R or the complex field C. In this paper we shall consider a semi-simple algebra 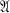= 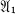⊕ … ⊕ 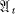over R or C with simple components 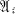. Let G be the group of all automorphisms or anti-automorphisms of 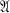which leave the ground field elementwise invariant, and let H be the subgroup of G such that Ω 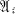= 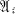(i = 1, 2, … , t) for each Ω in H.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 590 - 598
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Albert, A. A., Structure of algebras (Providence, 1939).Google Scholar
2. Cullen, C. G., Intrinsic functions on matrices of real quaternions, Can. J. Math., 15 (1963), 456–466.Google Scholar
3. Cullen, C. G. and Hall, C. A., Classes of functions on algebras, Can. J. Math., 18 (1966), 139–146.Google Scholar
4. Cullen, C. G. and Hall, C. A., Functions on semi-simple algebras, Amer. Math. Monthly, 74 (1967), 14–19.Google Scholar
5. Rinehart, R. F., Elements of intrinsic functions on algebras, Duke Math. J., 27 (1960), 1–20.Google Scholar
6. Rinehart, R. F., Intrinsic functions on matrices, Duke Math. J., 28 (1961), 291–300.Google Scholar
7. Rinehart, R. F., The equivalence of definitions of a matrix function, Amer. Math. Monthly, 62 (1955), 395–214.Google Scholar
8. Rinehart, R. F. and Wilson, J. C., Functions on algebras under homomorphic mappings, Duke Math. J., vol. 2 (1964), 221–227.Google Scholar
9. Ringleb, F., Beitrdge zur Funktionnetheorie in hypercomplexen Systemen, I, Rend. Circ. Mat. Palermo, 57 (1933), 311–340.Google Scholar