Article contents
Hankel Operators on Pseudoconvex Domains of Finite Type in ℂ2
Published online by Cambridge University Press: 20 November 2018
Abstract
The aim of this paper is to study small Hankel operators  $h$ on the Hardy space or on weighted Bergman spaces,where
$h$ on the Hardy space or on weighted Bergman spaces,where 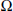 $\Omega $ is a finite type domain in
$\Omega $ is a finite type domain in 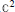 ${{\mathbb{C}}^{2}}$ or a strictly pseudoconvex domain in
${{\mathbb{C}}^{2}}$ or a strictly pseudoconvex domain in 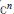 ${{\mathbb{C}}^{n}}$. We give a sufficient condition on the symbol
${{\mathbb{C}}^{n}}$. We give a sufficient condition on the symbol 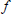 $f$ so that
$f$ so that  $h$ belongs to the Schatten class
$h$ belongs to the Schatten class 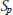 ${{S}_{p}}$,
${{S}_{p}}$, 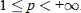 $1\,\le \,p\,<\,+\infty $.
$1\,\le \,p\,<\,+\infty $.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
References
- 2
- Cited by


