Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-18T21:11:27.593Z Has data issue: false hasContentIssue false
  • English
  • Français

Groups with the Subnormal Join Property

Published online by Cambridge University Press:  20 November 2018

Howard Smith
Howard Smith*
Affiliation:
University College, Cardiff, U.K.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A group G is said to have the subnormal join property (s.j.p.) if the join of two (and hence of finitely many) subnormal subgroups of G is always subnormal in G. Following Robinson [6], we shall denote the class of groups having this property by . A particular subclass of is 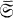, consisting of those groups G in which the join of two subnormals is again subnormal in G and has defect bounded in terms of the defects of the constituent subgroups (for a more precise definition see Section 7 of [6]).

In [16], Wielandt showed that groups which satisfy the maximal condition for subnormal subgroups have the s.j.p. Many further results on groups with the s.j.p. were proved in [6] and [7]. In Sections 2 and 3 of this paper, it will be shown that several of these results can be exhibited as corollaries of a few rather more general theorems on the classes , .

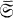Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 1 , 01 February 1985 , pp. 1 - 16
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Golovin, O. N., Nilpotent products of groups, Mat. Sb. 27 (1950), 427–454; Amer. Math. Soc. Transi., Ser 2, 2 (1956), 89–115.Google Scholar
2. Hall, P., Some sufficient conditions for a group to be nilpotent, Ill. J. 2 (1958), 787–801.Google Scholar
3. Heineken, H. and Mohamed, I. J., Groups with normalizer condition, Math. Ann. 198 (1972), 179–187.Google Scholar
4. Lennox, J. C., Segal, D. and Stonehewer, S. E., The lower central series of a join of subnormal subgroups, Math. Z. 154 (1977), 85–89.Google Scholar
5. Lennox, J. C. and Stonehewer, S. E., The join of two subnormal subgroups, J. Lond. Math. Soc. (2) 22 (1980), 460–466.Google Scholar
6. Robinson, D. J. S., Joins of subnormal subgroups, Ill. J. Math. 9 (1965), 144–168.Google Scholar
7. Robinson, D. J. S., On the theory of subnormal subgroups, Math. Z. 89 (1965), 30–51.Google Scholar
8. Robinson, D. J. S., Infinite soluble and nilpotent groups, London, Q.M.C. Math. Notes, (1968).Google Scholar
9. Robinson, D. J. S., Finiteness conditions and generalized soluble groups, (2 vols.), (Springer, Berlin, Heidelberg, New York, 1972).Google Scholar
10. Roseblade, J. E., On groups in which every subgroup is subnormal, J. Alg. 2 (1965), 402–412.Google Scholar
11. Roseblade, J. E., The derived series of a join of subnormal subgroups, Math. Z. 117 (1970), 57–69.Google Scholar
12. Roseblade, J. E. and Stonehewer, S. E., Subjunctive and locally coalescent classes of groups, J. Alg. 5 (1968), 423–435.Google Scholar
13. Smith, H., Commutator subgroups of a join of subnormal subgroups, Archiv der Mathematik 41 (1983), 193–198.Google Scholar
14. Stonehewer, S. E., The join of finitely many subnormal subgroups, Bull. Lond. Math. Soc. 2 (1970), 77–82.Google Scholar
15. Stonehewer, S. E., Nilpotent residuals of subnormal subgroups, Math. Z. 139 (1974), 45–54.Google Scholar
16. Wielandt, H., Eine Verallgemeinerung der invarianten Untergruppen, Math. Z. 45 (1939), 209–244.Google Scholar
17. Williams, J. P., The join of several subnormal subgroups, Proc. Cambridge Phil. Soc. 92 (1982), 391–399.Google Scholar
18. Zassenhaus, H., The theory of groups, 2nd ed. (Chelsea, 1958).Google Scholar