Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-26T23:33:48.870Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometric Classification of Graph C*-algebras over Finite Graphs

Published online by Cambridge University Press:  20 November 2018

Søren Eilers ,
Gunnar Restorff ,
Efren Ruiz  and
Adam P.W. Sørensen
Søren Eilers
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen, Denmark e-mail: eilers@math.ku.dk
Gunnar Restorff
Affiliation:
Department of Science and Technology, University of the Faroe Islands, Nóatún h, FO-00 Tórshavn, the Faroe Islands e-mail: gunnarr@setur.fo
Efren Ruiz
Affiliation:
Department of Mathematics, University of Hawaii, Hilo, 200 W.Kawili St., Hilo, Hawaii, 96720-4091 USA e-mail: ruize@hawaii.edu
Adam P.W. Sørensen
Affiliation:
Department of Mathematics, University of Oslo, PO BOX 1053 Blindern, N-0316 Oslo, Norway e-mail: apws@math.uio.no
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We address the classification problem for graph ${{C}^{*}}$-algebras of finite graphs (finitely many edges and vertices), containing the class of Cuntz-Krieger algebras as a prominent special case. Contrasting earlier work, we do not assume that the graphs satisfy the standard condition 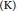$\left( K \right)$, so that the graph ${{C}^{*}}$-algebras may come with uncountably many ideals.

We find that in this generality, stable isomorphism of graph ${{C}^{*}}$-algebras does not coincide with the geometric notion of Cuntz move equivalence. However, adding a modest condition on the graphs, the two notions are proved to be mutually equivalent and equivalent to the C*-algebras having isomorphic 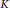$K$-theories. This proves in turn that under this condition, the graph ${{C}^{*}}$-algebras are in fact classifiable by 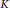$K$-theory, providing, in particular, complete classification when the ${{C}^{*}}$- algebras in question are either of real rank zero or type I/postliminal. The key ingredient in obtaining these results is a characterization of Cuntz move equivalence using the adjacency matrices of the graphs.

Our results are applied to discuss the classification problem for the quantumlens spaces defined by Hong and Szymański, and to complete the classification of graph ${{C}^{*}}$-algebras associated with all simple graphs with four vertices or less.

Keywords

46L8046L5537B10graph C*-algebrasgeometric classificationK-theoryflow equivalence
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 2 , 01 April 2018 , pp. 294 - 353
Copyright
Copyright © Canadian Mathematical Society 2018

References

[AAP08] Abrams, G. and Aranda Pino, G., The Leavitt path algebras of arbitrary graphs. Houston J. Math. (2008), no. 2, 423–442.Google Scholar
[ABAPMB+14] Alberca Bjerregaard, P., Aranda Pino, G., Martín Barquero, D., Martín González, C., and Siles Molina, M., Atlas of Leavitt path algebras of small graphs. J. Math. Soc. Japan (2014), no. 2, 581–611.http://dx.doi.org/10.2969/jmsj706620581 Google Scholar
[ABK14a] Arklint, S. E., Bentmann, R., and Katsura, T., The K-theoretical range of Cuntz-Krieger algebras. J. Funct. Anal. (2014), no. 8, 5448–5466.http://dx.doi.Org/10.1016/j.jfa.2O14.01.020 Google Scholar
[ABK14b] Arklint, S. E., Bentmann, R., and Katsura, T., Reduction of filtered K-theory and a characterization of Cuntz-Krieger algebras. J. K-Theory (2014), no. 3, 570–613.http://dx.doi.Org/10.1017/isOl4009013jkt281 Google Scholar
[ABL15] Arici, F., Brain, S., and Landi, G., The Gysin sequence for quantum lens spaces. J. Noncommut. Geom. (2015), no. 4, 1077–1111, http://dx.doi.org/10.4171/JNCC/216 Google Scholar
[APPSM09] Aranda Pino, G., Pardo, E., and Siles Molina, M., Prime spectrum and primitive Leavitt path algebras. Indiana Univ. Math. J. (2009), no. 2, 869–890.http://dx.doi.org/10.1512/iumj.2009.58.3516 Google Scholar
[AR15] Arklint, S. E. and Ruiz, E., Corners of Cuntz-Krieger algebras. Trans. Amer. Math. Soc. (2015), no. 11, 7595–7612.http://dx.doi.org/10.1090/S0002-9947-2015-06283-7 Google Scholar
[AT11] Abrams, G. and Tomforde, M., Isomorphism and Morita equivalence of graph algebras. Trans. Amer. Math. Soc. (2011), no. 7, 3733–3767.http://dx.doi.org/10.1090/S0002-9947-2011-05264-5 Google Scholar
[AT14] Abrams, G. and Tomforde, M., A class of C*-algebras that are prime but not primitive. Mönster J. Math. (2014), no. 2, 489–514.Google Scholar
[BHRS02] Bates, T., Hong, J. H., Raeburn, I., and Szymański, W., The ideal structure of the C*-algebras of infinite graphs. Illinois J. Math. (2002), no. 4,1159–1176.Google Scholar
[BP04] Bates, T. and Pask, D., Flow equivalence of graph algebras. Ergodic Theory Dynam. Systems (2004), no. 2, 367–382.http://dx.doi.org/10.1017/S0143385703000348 Google Scholar
[BlaO6] Blackadar, B., Operator algebras. Theory of C*-algebras and von Neumann algebras. In: Encyclopaedia of Mathematical Sciences, 122, Operator Algebras and Non-commutative Geometry , III, Springer-Verlag, Berlin, 2006.http://dx.doi.org/10.1007/3-540-28517-2 Google Scholar
[Boy02] Boyle, M., Flow equivalence of shifts of finite type via positive factorizations. Pacific J. Math. (2002), no. 2, 273–317. http://dx.doi.org/10.2140/pjm.2002.204.273 Google Scholar
[BH03] Boyle, M. and Huang, D., Poset block equivalence of integral matrices. Trans. Amer. Math. Soc. (2003), no. 10, 3861–3886. http://dx.doi.org/10.1090/S0002-9947-03-02947-7 Google Scholar
[Bro77] Brown, L. G., Stable isomorphism of hereditary subalgebras of C*-algebras. Pacific J. Math. (1977), no. 2, 335–348. http://dx.doi.Org/10.2140/pjm.1977.71.335 Google Scholar
[BCW17] Brownlowe, N., Carlsen, T. M., and Whittaker, M. F., Graph algebras and orbit equivalence. Ergodic Theory Dynam. Systems (2017), no. 2, 389–417.http://dx.doi.org/10.1017/etds.2015.52 Google Scholar
[BS16] Brzezinski, T. and Szymański, W., The C*-algebras of quantum lens and weighted projectivespaces. http://arxiv:1603.04678v1 Google Scholar
[CET12] Carlsen, T. M., Eilers, S., and Tomforde, M., Index maps in the K-theory of graph algebras. J. K-Theory (2012), no. 2, 385–406.http://dx.doi.Org/10.1017/isOl1004017jkt156 Google Scholar
[DHS03] Deicke, K., Hong, J. H., and Szymanski, W., Stable rank of graph algebras. Type I graph algebras and their limits. Indiana Univ. Math. J. (2003), no. 4, 963–979.http://dx.doi.Org/10.1512/iumj.2OO3.52.2350 Google Scholar
[DT05] Drinen, D. and Tomforde, M., The C*-algebras of arbitrary graphs. Rocky Mountain J. Math. (2005), no. 1, 105–135.http://dx.doi.org/10.1216/rmjm/1181069770 Google Scholar
[ERR13a] Eilers, S., Restorff, G., and Ruiz, E., Classifying C*-algebras with both finite and infinite subquotients. J. Funct. Anal. (2013), no. 3, 449–468.http://dx.doi.Org/10.1016/j.jfa.2013.05.006 Google Scholar
[ERR13b] Eilers, S., Restorff, G., and Ruiz, E., Strong classification of extensions of classifiable C*-algebras. http://arxiv:1301.7695v1 Google Scholar
[ERRS16a] Eilers, S., Restorff, G., Ruiz, E., and Sørensen, A. P. W., Invariance of the Cuntz splice. Math. Annalen, to appear. http://dx.doi.Org/10.1007/S00208-017-1570-Y Google Scholar
[ERRS16b] Eilers, S., Restorff, G., Ruiz, E., and Sorensen, A. P. W., The complete classification of unital graph C*-algebras: Geometric and strong. http://arxiv:1611.07120v1 Google Scholar
[ERRS17] Eilers, S., Restorff, G., Ruiz, E., and Sorensen, A. P. W., Filtered K-theory for graph algebras.2016 Matrix Annals, Springer, to appear.Google Scholar
[ERS12] Eilers, S., Ruiz, E., and Sørensen, A. P. W., Amplified graph C*-algebras. Münster J. Math. (2012), 121–150.Google Scholar
[FLROO] Fowler, N. J., Laca, M., and Raeburn, I., The C*-algebras of infinite graphs. Proc. Amer. Math. Soc. (2000), no. 8, 2319–2327.http://dx.doi.org/10.1090/S0002-9939-99-05378-2 Google Scholar
[Fra84] Franks, J., Flow equivalence ofsubshifts of finite type. Ergodic Theory Dynam. Systems (1984), no. 1, 53–66.http://dx.doi.org/10.1017/S0143385700002261 Google Scholar
[Gabl3] Gabe, J., Graph C*-algebras with a T1 primitive ideal space. In: Operator algebra and dynamics, Springer Proc. Math. Stat. , 58, Springer, Heidelberg, 2013, pp. 141–156.http://dx.doi.Org/10.1007/978-3-642-39459-1_7 Google Scholar
[HLM+14] Hay, D., Loving, M., Montgomery, M., Ruiz, E., and Todd, K., Non-stable K-theory for Leavittpath algebras. Rocky Mountain J. Math. (2014), no. 6,1817–1850.http://dx.doi.Org/10.1216/RMJ-2O14-44-6-1817 Google Scholar
[HS03b] Hong, J. H. and Szymański, W., Quantum lens spaces and graph algebras. Pacific J. Math. (2003), no. 2, 249–263. http://dx.doi.org/10.2140/pjm.2003.211.249 Google Scholar
[HS04] Hong, J. H. and Szymański, W., The primitive ideal space of the C*-algebras of infinite graphs. J. Math. Soc. Japan (2004), no. 1, 45–64.http://dx.doi.Org/10.2969/jmsj71191418695 Google Scholar
[Jeo04] Jeong, J. A., Real rank of C*-algebras associated with graphs. J. Aust. Math. Soc. (2004), no. 1, 141–147.http://dx.doi.org/10.1017/S1446788700010211 Google Scholar
[KirOO] Kirchberg, E., Das nicht-kommutative Michael-Auswahlprinzip und die Klassifikation nicht-einfacher Algebren. In: C*-algebras (Münster, 1999) , Springer, Berlin, 2000, pp. 92–141.Google Scholar
[KP99] Kumjian, A. and Pask, D., C*-algebras of directed graphs and group actions. Ergodic Theory Dynam. Systems (1999), no. 6,1503–1519.http://dx.doi.Org/10.1017/S0143385799151940 Google Scholar
[MM14] Matsumoto, K. and Matui, H., Continuous orbit equivalence of topological Markov shifts and Cuntz-Krieger algebras. Kyoto J. Math. (2014), no. 4, 863–877.http://dx.doi.Org/10.1215/21562261-2801849 Google Scholar
[MP14] McKay, B. D. and Piperno, A., Practical graph isomorphism, II. J. Symbolic Comput. (2014), 94–112.http://dx.doi.org/10.1016/J.JSC.2O13.09.003 Google Scholar
[MN09] Meyer, R. and Nest, R., C*-algebras over topological spaces: the bootstrap class. Münster J. Math. (2009), 215–252.Google Scholar
[Min87] Mingo, J. A., K-theory and multipliers of stable C*-algebras. Trans. Amer. Math. Soc. (1987), no. 1, 397–411. http://dx.doi.Org/10.2307/2000501 Google Scholar
[Mur90] Murphy, G. J., C*-algebras and operator theory.Academic Press, Inc., Boston, MA, 1990.Google Scholar
[PS75] Parry, B. and Sullivan, D., A topological invariant of flows on 1-dimensional spaces. Topology (1975), no. 4, 297–299. http://dx.doi.Org/10.1016/0040-9383(75)90012-9 Google Scholar
[Phi00] Phillips, N. C., A classification theorem for nuclear purely infinite simple C*-algebras. Doc. Math. (2000), 49–114.Google Scholar
[RaeO5] Raeburn, I., Graph algebras. CBMS Regional Conference Series in Mathematics , 103, Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 2005. http://dx.doi.Org/10.1090/cbms/103 Google Scholar
[ResO6] Restorff, G., Classification of Cuntz-Krieger algebras up to stable isomorphism. J. Reine Angew. Math. (2006), 185–210. http://dx.doi.org/10.1515/CRELLE.2006.074 Google Scholar
[Rør91] Rørdam, M., Ideals in the multiplier algebra of a stable C* -algebra. J. Operator Theory (1991), no. 2, 283–298.Google Scholar
[Rør95] Rørdam, M., Classification of Cuntz-Krieger algebras. Jf-Theory (1995), no. 1, 31–58.http://dx.doi.org/10.1007/BF00965458 Google Scholar
[RS87] Rosenberg, J. and Schochet, C., The Künneth theorem and the universal coefficient theorem for Kasparov's generalized K-functor. Duke Math. J. (1987), no. 2, 431–474.http://dx.doi.org/10.1215/S0012-7094-87-05524-4 Google Scholar
[RT13a] Ruiz, E. and Tomforde, M., Classification of unital simple Leavitt path algebras of infinite graphs. J. Algebra (2013), 45–83.http://dx.doi.Org/10.1016/j.jalgebra.2013.03.004 Google Scholar
[RT13b] Ruiz, E. and Tomforde, M., Ideal-related K-theory for Leavitt path algebras and graph C*-algebras. Indiana Univ. Math. J. (2013), no. 5,1587–1620.http://dx.doi.Org/10.1512/iumj.2013.62.5123 Google Scholar
[Slo] Sloane, N. J. A., The on-line encyclopedia of integer sequences, http://oeis.org Google Scholar
[Sørl3] Sørensen, A. P. W., Geometric classification of simple graph algebras. Ergodic Theory Dynam. Systems (2013), no. 4,1199–1220.http://dx.doi.Org/10.1017/S0143385712000260 Google Scholar
[SzyO2] Szymański, W., General Cuntz-Krieger uniqueness theorem. Internat. J. Math. (2002), no. 5, 549–555.http://dx.doi.Org/10.1142/S0129167X0200137X Google Scholar
[Tom03] Tomforde, M., The ordered K0-group of a graph C* -algebra. C. R. Math. Acad. Sci. Soc. R. Can. (2003), no. 1,19–25.Google Scholar
[WeaO3] Weaver, N., Aprime C* -algebra that is not primitive. J. Funct. Anal. (2003), no. 2, 356–361.http://dx.doi.org/10.1016/SOO22-1236(03)00196-4 Google Scholar