Hostname: page-component-848d4c4894-p2v8j Total loading time: 0.001 Render date: 2024-05-26T04:54:26.359Z Has data issue: false hasContentIssue false
  • English
  • Français

The General Definition of the Complex Monge–Ampère Operator on Compact Kähler Manifolds

Part of: Differential operators in several variables Complex manifolds

Published online by Cambridge University Press:  20 November 2018

Yang Xing
Yang Xing*
Affiliation:
Centre for Mathematical Sciences, Lund University, SE-22100, Lund, Sweden, e-mail: yang.xing@math.lth.se
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce a wide subclass 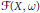$\mathcal{F}\left( X,\,\omega \right)$ of quasi-plurisubharmonic functions in a compact Kähler manifold, on which the complex Monge-Ampère operator is well defined and the convergence theorem is valid. We also prove that 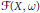$\mathcal{F}\left( X,\,\omega \right)$ is a convex cone and includes all quasi-plurisubharmonic functions that are in the Cegrell class.

Keywords

complex Monge-Ampère operatorcompact Kähler manifold

MSC classification

Secondary: 32W20: Complex Monge-Ampère operators 32Q15: Kähler manifolds
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 1 , 01 February 2010 , pp. 218 - 239
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] E., Bedford, Survey of pluri-potential theory. In: Several Complex Variables. Math. Notes 38, Princeton University Press, Princeton, NJ, 1993, pp. 48-97.Google Scholar
[2] E., Bedford and B. A., Taylor, A new capacity for plurisubharmonic functions. Acta Math. 149(1982), no. 1-2, 1-40. doi:10.1007/BF02392348Google Scholar
[3] E., Bedford and B. A., Taylor, Fine topology, Šilov boundary and (ddc)n. J. Funct. Anal. 72(1987), no. 2, 225-251. doi:10.1016/0022-1236(87)90087-5Google Scholar
[4] Z., Błocki, Uniqueness and stability of the complex Monge-Ampère operator on compact Kähler manifolds. Indina Univ. Math. J. 52(2003), no. 6, 1697-1701. doi:10.1512/iumj.2003.52.2346Google Scholar
[5] Z., Błocki, The domain of definition for the complex Monge-Ampère operator. Amer. J. Math. 128(2006), no. 2, 519-530. doi:10.1353/ajm.2006.0010Google Scholar
[6] Z., Błocki and Kołodziej, S., On regularization of plurisubharmonic functions on manifolds. Proc. Amer. Math. Soc. 135(2007), no. 7, 2089-2093. doi:10.1090/S0002-9939-07-08858-2Google Scholar
[7] U., Cegrell, Pluricomplex energy. Acta Math. 180(1998), no. 2, 187-217. doi:10.1007/BF02392899Google Scholar
[8] U., Cegrell, The general definition of the complex Monge-Ampère operator. Ann. Inst. Fourier (Grenoble) 54(2004), no. 1, 159-179.Google Scholar
[9] Demailly, J.-P., Regularization of closed positive currents and intersection theory. J. Algebraic Geom. 1(1992), 361-409.Google Scholar
[10] V., Guedj and A., Zeriahi, The weighted Monge-Ampère energy of quasiplurisubharmonic functions. J. Funct. Anal. 250(2007), no. 2, 442-482. doi:10.1016/j.jfa.2007.04.018Google Scholar
[11] N. V., Khue and P. H., Hiep, Some properties of the complex Monge-Ampère operator in Cegrell's classes and applications. www.arXiv.org:0704.0359. Google Scholar
[12] C. O., Kiselman, Sur la définition de l'opérateur de Monge-Ampère complexe. In: Analyse Complexe. Lecture Notes in Math. 1094. Springer, Berlin, 1984, pp. 139-150.Google Scholar
[13] S., Kołodziej, The complex Monge-Ampère equation and pluripotential theory. Mem. Amer. Math. Soc. 178(2005), no. 840.Google Scholar
[14] S., Kołodziej, The set of measures given by bounded solutions of the complex Monge-Ampère equation on compact Kähler manifolds. J. London Math. Soc. 72(2005), no. 1, 225-238. doi:10.1112/S0024610705006460Google Scholar
[15] Y., Xing, Continuity of the complex Monge-Ampère operator. Proc. Amer.Math. Soc. 124(1996), no. 2, 457-467. doi:10.1090/S0002-9939-96-03316-3Google Scholar
[16] Y., Xing, Convergence in capacity. Ann. Inst. Fourier (Grenoble) 58(2008), no. 5, 1839-1861.Google Scholar
[17] Y., Xing, Continuity of the complex Monge-Ampère operator on compact Kähler manifolds.Math. Z. 263(2009), 331-344.Google Scholar