Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-16T11:55:58.569Z Has data issue: false hasContentIssue false
  • English
  • Français

Galois Representations with Non-Surjective Traces

Published online by Cambridge University Press:  20 November 2018

Chantal David ,
Hershy Kisilevsky  and
Francesco Pappalardi
Chantal David
Affiliation:
Concordia University, Department of Mathematics, 1455 de Maisonneuve Blvd. West, Montréal, Quebec, H3G 1M8 email: chantal@cicma.concordia.ca
Hershy Kisilevsky
Affiliation:
Concordia University, Department of Mathematics, 1455 de Maisonneuve Blvd. West, Montréal, Quebec, H3G 1M8 email: kisilev@cicma.concordia.ca
Francesco Pappalardi
Affiliation:
Università degli Studi di Roma Tre, Dipartimento di Matematica, Via Corrado Segre, 4, 00146 Roma, Italy email: pappa@mat.uniroma3.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $E$ be an elliptic curve over 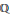$\mathbb{Q}$ , and let $r$ be an integer. According to the Lang-Trotter conjecture, the number of primes 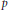$p$ such that 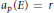${{a}_{p}}\left( E \right)=r$ is either finite, or is asymptotic to 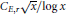${{C}_{E,r}}\sqrt{x}/\log x$ where 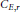${{C}_{E,r}}$ is a non-zero constant. A typical example of the former is the case of rational $\ell $-torsion, where 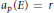${{a}_{p}}\left( E \right)=r$ is impossible if 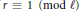$r\equiv 1\,\left( \bmod \,\ell \right)$. 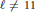We prove in this paper that, when $E$ has a rational $\ell $-isogeny and $\ell \ne 11$, the number of primes 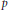$p$ such that 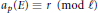${{a}_{p}}\left( E \right)\equiv r\,\left( \bmod \,\ell \right)$ is finite (for some $r$ modulo $\ell $) if and only if $E$ has rational $\ell $-torsion over the cyclotomic field 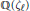$\mathbb{Q}\left( {{\zeta }_{\ell }} \right)$ . The case 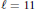$\ell =11$ is special, and is also treated in the paper. We also classify all those occurences.

Keywords

14H52
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 5 , 01 October 1999 , pp. 936 - 951
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Modular functions of one variable VI (eds. Serre, J.-P. and Zagier, D. B.). Proceedings of the Second International Conference, held at the University of Bonn, Bonn, July 2–14, 1976. Lecture Notes in Math. 627, Springer-Verlag, Berlin-New York, 1977.Google Scholar
[2] Batut, C., Belabas, K., Bernardi, D., Cohen, H. and Olivier, M., PARI-GP. Google Scholar
[3] Coleman, R., Effective Chabauty. Duke Math. J. 52(1985), 765–770.Google Scholar
[4] Cremona, J. E., Algorithms for modular elliptic curves. Cambridge University Press, 1992.Google Scholar
[5] David, C. and Pappalardi, F., Average Frobenius distributions of elliptic curves. Internat. Math. Res. Notices 4(1999), 165–183.Google Scholar
[6] Deuring, M., Die Typen derMultiplikatorenringe elliptischer Funktionenkörper. Abh.Math. Sem. Hansischen Univ. 14(1941), 197–272.Google Scholar
[7] Duke, W., Rational elliptic curves with no exceptional primes. C. R. Acad. Sci. Paris 325(1997), 813–818.Google Scholar
[8] Grant, D., A formula for the number of elliptic curves with exceptional primes. Compositio Math., to appear.Google Scholar
[9] Lang, S. and Trotter, H., Frobenius distributions in GL2-extensions. Lecture Notes in Math. 504, Springer-Verlag, 1976.Google Scholar
[10] Mazur, B., Modular curves and the Eiseinstein ideal. Inst. Hautes Études Sci. Publ. Math. 47(1977), 33–186.Google Scholar
[11] Mazur, B., Rational isogenies of prime degree. Invent.Math. 44(1978), 129–162.Google Scholar
[12] Mazur, B. and Swinnerton-Dyer, P., Arithmetic of Weil curves. Invent.Math. 25(1974), 1–61.Google Scholar
[13] Momose, F., p-torsion points on elliptic curves defined over quadratic fields. Nagoya Math. J. 96(1984), 115–137.Google Scholar
[14] Ogg, A. P., Rational points on certain elliptic modular curves. Proc. Symp. Pure Math. 24(1973), 221–231.Google Scholar
[15] Serre, J.-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques. Invent.Math. 15(1972), 259–331.Google Scholar
[16] Silverman, J., The arithmetic of elliptic curves. Springer-Verlag, 1986.Google Scholar
[17] Stark, H., Counting points on CM elliptic curves. Rocky Mountain J. Math. 26(1996), 1115–1138.Google Scholar