No CrossRef data available.
Article contents
The Frobenius semiradical, generic stabilizers, and Poisson center for nilradicals
Published online by Cambridge University Press: 27 October 2023
Abstract
Let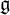 
${\mathfrak g}$ be a complex simple Lie algebra and 
${\mathfrak n}$ the nilradical of a parabolic subalgebra of 
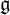${\mathfrak g}$. We consider some properties of the coadjoint representation of 
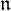${\mathfrak n}$ and related algebras of invariants. This includes (i) the problem of existence of generic stabilizers, (ii) a description of the Frobenius semiradical of 
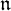${\mathfrak n}$ and the Poisson center 
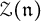of the symmetric algebra 
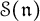, (iii) the structure of 
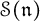as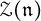 
-module, and (iv) the description of square integrable (= quasi-reductive) nilradicals. Our main technical tools are the Kostant cascade in the set of positive roots of 
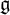${\mathfrak g}$ and the notion of optimization of 
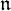${\mathfrak n}$.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
References
Baur, K. and Moreau, A., Quasi-reductive (bi)parabolic subalgebras of reductive lie algebras. Ann. Inst. Fourier. 61(2011), no. 2, 417–451.CrossRefGoogle Scholar
Brion, M., Sur la thèorie des invariants. Publ. Math. Univ. Pierre et Marie Curie. 45(1981), 1–92.Google Scholar
Brion, M., Surfaces quotients par un groupe unipotent. Comm. Algebra 11(1983), no. 9, 1011–1014.CrossRefGoogle Scholar
Brion, M.,
Invariants et covariants des groupes algébriques réductifs
. In: Théorie des invariants et géometrie des variétés quotients, Travaux en cours, 61, Hermann, Paris, 2000, pp. 83–168.Google Scholar
Dixmier, J., Enveloping algebras, American Mathematical Society, Providence, RI, 1996, xx + 379 pp.Google Scholar
Duflo, M., Théorie de Mackey pour les groupes de lie algébriques. Acta Math. 149(1982), 153–213.CrossRefGoogle Scholar
Duflo, M., Khalgui, M. S., and Torasso, P., Algèbres de lie quasi-réductives. Transform. Groups 17(2012), no. 2, 417–470.CrossRefGoogle Scholar
Elashvili, A. G., Canonical form and stationary subalgebras of points of general position for simple linear lie groups. Funct. Anal. Appl. 6(1972), 44–53.CrossRefGoogle Scholar
Elashvili, A. G., On the index of horospherical subalgebras of semisimple Lie algebras. Trudy Razmadze Math. Inst. (Tbilisi) 77(1985), 116–126 (in Russian).Google Scholar
Elashvili, A. G. and Ooms, A., On commutative polarizations. J. Algebra 264(2003), 129–154.CrossRefGoogle Scholar
Grosshans, F., Algebraic homogeneous spaces and invariant theory, Lecture Notes in Mathematics, 1673, Springer, Berlin, 1997.CrossRefGoogle Scholar
Joseph, A., A preparation theorem for the prime spectrum of a semisimple Lie algebra. J. Algebra 48(1977), 241–289.CrossRefGoogle Scholar
Kostant, B., The cascade of orthogonal roots and the coadjoint structure of the nilradical of a Borel subgroup of a semisimple Lie group. Mosc. Math. J. 12(2012), no. 3, 605–620.CrossRefGoogle Scholar
Kraft, H., Geometrische Methoden in der Invariantentheorie, Aspekte der Mathematik, D1, Vieweg & Sohn, Braunschweig, 1984.CrossRefGoogle Scholar
Moore, C. C. and Wolf, J. A., Square integrable representations of nilpotent groups. Trans. Amer. Math. Soc. 185(1973), 445–462.CrossRefGoogle Scholar
Moreau, A. and Yakimova, O., Coadjoint orbits of reductive type of parabolic and seaweed lie subalgebras. Int. Math. Res. Not. IMRN 2012(2012), no. 19, 4475–4519.Google Scholar
Onishchik, A. L. and Vinberg, E. B., Lie groups and algebraic groups, Springer, Berlin, 1990.CrossRefGoogle Scholar
Ooms, A., On certain maximal subfields in the quotient division ring of an enveloping algebra. J. Algebra 230(2000), no. 2, 694–712.CrossRefGoogle Scholar
Ooms, A., The Frobenius semiradical of a Lie algebra. J. Algebra 273(2004), no. 1, 274–287.CrossRefGoogle Scholar
Panyushev, D., Parabolic subgroups with abelian unipotent radical as a testing site for invariant theory. Canad. J. Math. 51(1999), no. 3, 616–635.CrossRefGoogle Scholar
Panyushev, D., On the orbits of a Borel subgroup in abelian ideals. Transform. Groups 22(2017), no. 2, 503–524.CrossRefGoogle Scholar
Panyushev, D., Commutative polarisations and the Kostant cascade. Algebr. Represent. Theory 26(2023), no. 3, 967–985.CrossRefGoogle Scholar
Popov, V. L., Contractions of actions of reductive algebraic groups. Math. USSR-Sb. 58(1987), 311–335.CrossRefGoogle Scholar
Richardson, R. W., Principal orbit types for algebraic transformation spaces in characteristic zero. Invent. Math. 16(1972), 6–14.CrossRefGoogle Scholar
Sadetov, S. T., A proof of the Mishchenko–Fomenko conjecture. Doklady Math. 70(2004), no. 1, 634–638.Google Scholar
Schwarz, G., Lifting smooth homotopies of orbit spaces. Publ. Math. I.H.E.S. 51(1980), 37–135.CrossRefGoogle Scholar
Tauvel, P. and Yu, R., Indice et formes linéaires stables dans les algèbres de lie. J. Algebra 273(2004), 507–516.CrossRefGoogle Scholar
Vinberg, E. B., On certain commutative subalgebras of a universal enveloping algebra. Math. USSR-Izv. 36(1991), 1–22.CrossRefGoogle Scholar
Vinberg, E. B. and Gindikin, S. G., Degeneration of horospheres in spherical homogeneous spaces. Funct. Anal. Appl. 52(2018), 83–92.CrossRefGoogle Scholar