No CrossRef data available.
Article contents
Exponents of Diophantine Approximation in Dimension Two
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let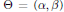 
$\Theta \,=\,\left( \alpha ,\,\beta \right)$ be a point in 
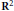${{\text{R}}^{2}}$, with 
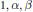$1,\,\alpha ,\,\beta $ linearly independent over 
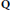$\mathrm{Q}$. We attach to 
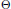$\Theta $ a quadruple 
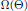$\Omega \left( \Theta \right)$ of exponents that measure the quality of approximation to 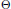$\Theta $ both by rational points and by rational lines. The two “uniform” components of 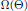$\Omega \left( \Theta \right)$ are related by an equation due to Jarník, and the four exponents satisfy two inequalities that refine Khintchine's transference principle. Conversely, we show that for any quadruple 
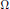$\Omega $ fulfilling these necessary conditions, there exists a point 
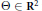$\Theta \,\in \,{{\text{R}}^{2}}$ for which 
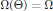$\Omega \left( \Theta \right)\,=\,\Omega $.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2009
References
[1]
Baker, R. C., Singular n-tuples and Hausdorff dimension. II. Math. Proc. Cambridge Philos. Soc. 111 (1992), no. 3, 577–584.Google Scholar
[2]
Bombieri, E. and Vaaler, J., On Siegel's lemma. Invent. Math. 73 (1983), no. 1, 11–32.Google Scholar
[3]
Bugeaud, Y. and Laurent, M., Exponents of Diophantine approximation and Sturmian continued fractions. Ann. Inst. Fourier 55 (2005), no. 3, 773–804.Google Scholar
[4]
Bugeaud, Y. and Laurent, M., On exponents of homogeneous and inhomogeneous Diophantine approximation. Mosc. Math. J. 5 (2005), no. 4, 747–766.Google Scholar
[5]
Bugeaud, Y. and Laurent, M., Exponents of Diophantine approximation. In: Diophantine geometry, CRM Series 4, Ed. Norm., Pisa, 2007, pp. 101–121.Google Scholar
[6]
Davenport, H. and Schmidt, W. M., Approximation to real numbers by algebraic integers. Acta Arith. 15 (1968/1969), 393–416.Google Scholar
[7]
Fischler, S., Spectres pour l’approximation d’un nombre réel et de son carré. C. R. Math. Acad. Sci. Paris 339 (2004), no. 10, 679–682.Google Scholar
[9]
Jarnìk, V., O simultánních diofantickych approximacích, Rozpravy Tŕ. České Akad 45, c. 19 (1936), 16 pp.Google Scholar
[10]
Jarnìk, V., Über ein Satz von A. Khintchine, 2. Mitteilung. Acta Arith. 2 (1936), 1–22.Google Scholar
[11]
Jarnìk, V., Zum Khintchineschen “Übertragungssatz”. Trav. Inst. Math. Tbilissi 3 (1938), 193–212.Google Scholar
[12]
Jarnìk, V., Une remarque sur les approximations diophantiennes linéaires. Acta Sci.Math. Szeged 12 (1950), 82–86.Google Scholar
[13]
Jarnìk, V., Contribution à la théorie des approximations diophantiennes linéaires et homogènes. Czechoslovak Math. J. 4 (1954), no. 79, 330–353.Google Scholar
[14]
Khintchine, A. J., Über eine Klasse linearer diophantischer Approximationen. Rendiconti Circ. Mat. Palermo 50 (1926), 170–195.Google Scholar
[15]
Lagarias, J. C., Best Diophantine approximations to a set of linear forms. J. Austral.Math. Soc. Ser. A 34 (1983), no. 1, 114–122.Google Scholar
[16]
Roy, D., Approximation to real numbers by cubic algebraic integers, I. Proc. London Math. Soc. 88 (2004), no. 1, 42–62.Google Scholar
[17]
Roy, D., Diophantine approximation in small degree.
Number Theory, CRM Proc. Lecture Notes 36, American Mathematical Society, Providence, RI, 2004, pp. 269–285.Google Scholar
[18]
Roy, D., On two exponents of approximation related to a real number and its square. Canad. J. Math. 59 (2007), no. 11, 211–224.Google Scholar
[19]
Rynne, B. P., A lower bound for the Hausdorff dimension of sets of singular n-tuples. Math. Proc. Cambridge Philos. Soc. 107 (1990), no. 2, 387–394.Google Scholar
[20]
Schmidt, W. M., On heights of algebraic subspaces and diophantine approximations. Ann. of Math. 85 (1967), 430–472.Google Scholar
You have
Access
- 9
- Cited by