Article contents
The Cuntz semigroup of unital commutative AI-algebras
Published online by Cambridge University Press: 18 October 2022
Abstract
We provide an abstract characterization for the Cuntz semigroup of unital commutative AI-algebras, as well as a characterization for abstract Cuntz semigroups of the form 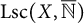 $\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}})$ for some
$\operatorname {\mathrm {Lsc}} (X,\overline {\mathbb {N}})$ for some 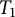 $T_1$-space X. In our investigations, we also uncover new properties that the Cuntz semigroup of all AI-algebras satisfies.
$T_1$-space X. In our investigations, we also uncover new properties that the Cuntz semigroup of all AI-algebras satisfies.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
The author was partially supported by the MINECO (Grant Nos. PRE2018-083419 and MTM2017-83487-P) and by the Comissionat per Universitats i Recerca de la Generalitat de Catalunya (Grant No. 2017SGR01725).
References
- 3
- Cited by





