Hostname: page-component-84b7d79bbc-g7rbq Total loading time: 0 Render date: 2024-07-26T23:18:28.694Z Has data issue: false hasContentIssue false
  • English
  • Français

Covering Linkage Invariants

Published online by Cambridge University Press:  20 November 2018

Richard Hartley  and
Kunio Murasugi
Richard Hartley
Affiliation:
University of Toronto, Toronto, Ontario
Kunio Murasugi
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

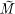Let K be a knot in a manifold M. Corresponding to a representation of Π1(M — K) into a transitive group of permutations there is a branched covering space of M. K is covered by 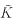which may be a link of several components. The set of linking numbers between the various components of 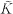has long been recognised as a useful knot invariant. Bankwitz and Schumann used this invariant in considering dihedral coverings of Viergeflechte.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 6 , 01 December 1977 , pp. 1312 - 1339
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Bankwitz and Schumann, Uber Viergeflechte, Abh. Math. Sem. Univ. Hamburg 10 (1934), 263–284.Google Scholar
2. Bing, R. and Martin, M., Cubes with knotted holes, Trans. Amer. Math. Soc. 155 (1971), 217–231.Google Scholar
3. Burde, G., Darstellungen von Knotengruppen, Math. Annalen 173 (1967), 24–33.Google Scholar
4. Cappell, S. E. and Shaneson, J. L., Invariants of 3-manifolds, Bull. A.M.S. 81 (1975), 559–562.Google Scholar
5. Crowell and Fox, An introduction to knot theory (Ginn and Co., 1963).Google Scholar
6. Fox, R., Metacydic invariants of knots and links, Can. J. Math. 22 (1970), 193–201.Google Scholar
7. Fox, R. A quick trip through knot theory, Topology of Three Manifolds and Related Topics (Prentice Hall, 1962), 120–167.Google Scholar
8. Gonzalez-Acuna, F., Dehns construction on knots, Boletin de la Scoiedad Mathematica Mexicana 15 (1970), 58–79.Google Scholar
9. Hempel, J., A simply connected 3-Manifold is S* if it is the sum of a solid torus and the complement of a torus knot, Proc. Amer. Math. Soc. 15 (1964), 154–158.Google Scholar
10. Magnus, W., A. Karrass and Solitar, D., Combinatorial group theory (Interscience, 1966).Google Scholar
11. Montesinos, J. M., Sobre la Conjetura de Poincaré y los recubridores ramificados sobre unnudo, Tesis doctoral, Madrid, 1971.Google Scholar
12. Perko, K., On covering spaces of knots, Glasnik Matematicki, 9 (29) (1974), 141–145.Google Scholar
13. Perko, K. On the classification of knots. Proc. Amer. Math. Soc. Jf.5 (1974), 262–266.Google Scholar
14. Perko, K. On dihedral covering spaces of knots, Inventiones Math. 34 (1976), 77–82.Google Scholar
15. Reyner, S. W., On metabelian and related invariants of knots, Ph.D. thesis, Princeton, 1972.Google Scholar
16. Riley, R., Homomorphisms of knot groups on finite groups, Mathematics of Computation 25 (1971), 603–619.Google Scholar
17. Riley, R. Knots with the parabolic property P, Oxford Quarterly Journal of Math. 25 (1974), 273–283.Google Scholar
18. Schubert, H., Topology (Allyn and Bacon, 1968).Google Scholar
19. Seifert, H., Topologie dreidimensionaler gefaserter Raume, Acta Math. 60 (1933), 147–238.Google Scholar