Article contents
BMO Functions and Carleson Measures with Values in Uniformly Convex Spaces
Published online by Cambridge University Press: 20 November 2018
Abstract
This paper studies the relationship between vector-valued 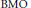 $\text{BMO}$ functions and the Carleson measures defined by their gradients. Let
$\text{BMO}$ functions and the Carleson measures defined by their gradients. Let 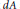 $dA$ and
$dA$ and 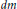 $dm$ denote Lebesgue measures on the unit disc
$dm$ denote Lebesgue measures on the unit disc 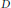 $D$ and the unit circle
$D$ and the unit circle 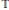 $\mathbb{T}$, respectively. For
$\mathbb{T}$, respectively. For 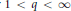 $1\,<\,q\,<\,\infty $ and a Banach space
$1\,<\,q\,<\,\infty $ and a Banach space 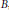 $B$, we prove that there exists a positive constant
$B$, we prove that there exists a positive constant  $c$ such that
$c$ such that
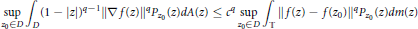 $$\underset{{{z}_{0}}\in D}{\mathop{\sup }}\,{{\int }_{D}}{{\left( 1-\left| z \right| \right)}^{q-1}}{{\left\| \nabla f\left( z \right) \right\|}^{q}}{{P}_{{{Z}_{0}}}}\left( z \right)dA\left( z \right)\le {{c}^{q}}\underset{{{z}_{0}}\in D}{\mathop{\sup }}\,{{\int }_{\mathbb{T}}}{{\left\| f\left( z \right)-f\left( {{z}_{0}} \right) \right\|}^{q}}{{P}_{{{z}_{0}}}}\left( z \right)dm\left( z \right)$$
$$\underset{{{z}_{0}}\in D}{\mathop{\sup }}\,{{\int }_{D}}{{\left( 1-\left| z \right| \right)}^{q-1}}{{\left\| \nabla f\left( z \right) \right\|}^{q}}{{P}_{{{Z}_{0}}}}\left( z \right)dA\left( z \right)\le {{c}^{q}}\underset{{{z}_{0}}\in D}{\mathop{\sup }}\,{{\int }_{\mathbb{T}}}{{\left\| f\left( z \right)-f\left( {{z}_{0}} \right) \right\|}^{q}}{{P}_{{{z}_{0}}}}\left( z \right)dm\left( z \right)$$
holds for all trigonometric polynomials 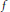 $f$ with coefficients in
$f$ with coefficients in 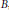 $B$ if and only if
$B$ if and only if 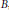 $B$ admits an equivalent norm which is
$B$ admits an equivalent norm which is  $q$-uniformly convex, where
$q$-uniformly convex, where
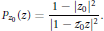 $${{P}_{{{z}_{0}}}}\left( z \right)=\frac{1-|{{z}_{0}}{{|}^{2}}}{|1-{{{\bar{z}}}_{0}}z{{|}^{2}}}.$$
$${{P}_{{{z}_{0}}}}\left( z \right)=\frac{1-|{{z}_{0}}{{|}^{2}}}{|1-{{{\bar{z}}}_{0}}z{{|}^{2}}}.$$
The validity of the converse inequality is equivalent to the existence of an equivalent  $q$-uniformly smooth norm.
$q$-uniformly smooth norm.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010
References
- 5
- Cited by




