In 2007, Andrews introduced Durfee symbols and k-marked Durfee symbols so as to give a combinatorial interpretation for the symmetrized moment function 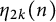$\eta _{2k}(n)$ of ranks of partitions. He also considered the relations between odd Durfee symbols and the mock theta function 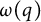$\omega (q)$, and proved that the 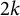$2k$th moment function 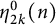$\eta _{2k}^0(n)$ of odd ranks of odd Durfee symbols counts 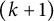$(k+1)$-marked odd Durfee symbols of n. In this paper, we first introduce the definition of symmetrized positive odd rank moments 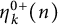$\eta _k^{0+}(n)$ and prove that for all 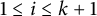$1\leq i\leq k+1$, 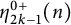$\eta _{2k-1}^{0+}(n)$ is equal to the number of 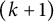$(k+1)$-marked odd Durfee symbols of n with the ith odd rank equal to zero and 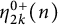$\eta _{2k}^{0+}(n)$ is equal to the number of 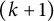$(k+1)$-marked Durfee symbols of n with the ith odd rank being positive. Then we calculate the generating functions of 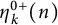$\eta _{k}^{0+}(n)$ and study its asymptotic behavior. Finally, we use Wright’s variant of the Hardy–Ramanujan circle method to obtain an asymptotic formula for 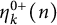$\eta _{k}^{0+}(n)$.