Hostname: page-component-6d856f89d9-mhpxw Total loading time: 0 Render date: 2024-07-16T08:53:39.102Z Has data issue: false hasContentIssue false
  • English
  • Français

An Lp Saturation Theorem for Splines

Published online by Cambridge University Press:  20 November 2018

G. J. Butler  and
F. B. Richards
G. J. Butler
Affiliation:
University of Alberta, Edmonton, Alberta
F. B. Richards
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 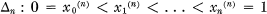1 be a subdivision of [0, 1], and let 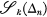denote the class of functions whose restriction to each sub-interval 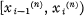is a polynomial of degree at most k. Gaier [1] has shown that for uniform subdivisions △n (that is, subdivisions for which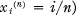

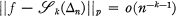
if and only if f is a polynomial of degree at most k. Here, and subsequently, 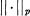denotes the usual norm in Lp[0, 1], 1 ≦ p ≦ ∞, and we should emphasize that functions differing only on a set of Lebesgue measure zero are identified.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 24 , Issue 5 , October 1972 , pp. 957 - 966
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Gaier, D., Saturation bei Spline-Approximation und Quadratur, Numer. Math. 16 (1970), 129–140.Google Scholar
2. Hardy, G. H. and Littlewood, J. E., Some properties of fractional integrals, Math. Z. 27 (1928), 565–606.Google Scholar
3. Popov, V. and Sendov, Bl., Classes characterized by best possible approximations by spline functions, Math. Notes No. 2, 18 (1970), 550–557.Google Scholar
4. Richards, F., On the saturation class for spline functions (to appear in Proc. Amer. Math. Soc, May 1972).Google Scholar
5. Riesz, F., Systeme integrierbarer Funktionen, Math. Ann. 69 (1910), 449–497.Google Scholar
6. Schoenberg, I. J., On interpolation by spline functions and its minimal properties, On Approximation Theory (Intern. Ser. Numerical Math. (ISNM) 5 (1964), 109–129, Birkhauser, Basel/Stuttgart).Google Scholar