Article contents
Ring-theoretic (In)finiteness in reduced products of Banach algebras
Published online by Cambridge University Press: 29 June 2020
Abstract
We study ring-theoretic (in)finiteness properties—such as Dedekind-finiteness and proper infiniteness—of ultraproducts (and more generally, reduced products) of Banach algebras.
While we characterise when an ultraproduct has these ring-theoretic properties in terms of its underlying sequence of algebras, we find that, contrary to the 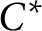 $C^*$
-algebraic setting, it is not true in general that an ultraproduct has a ring-theoretic finiteness property if and only if “ultrafilter many” of the underlying sequence of algebras have the same property. This might appear to violate the continuous model theoretic counterpart of Łoś’s Theorem; the reason it does not is that for a general Banach algebra, the ring theoretic properties we consider cannot be verified by considering a bounded subset of the algebra of fixed bound. For Banach algebras, we construct counter-examples to show, for example, that each component Banach algebra can fail to be Dedekind-finite while the ultraproduct is Dedekind-finite, and we explain why such a counter-example is not possible for
$C^*$
-algebraic setting, it is not true in general that an ultraproduct has a ring-theoretic finiteness property if and only if “ultrafilter many” of the underlying sequence of algebras have the same property. This might appear to violate the continuous model theoretic counterpart of Łoś’s Theorem; the reason it does not is that for a general Banach algebra, the ring theoretic properties we consider cannot be verified by considering a bounded subset of the algebra of fixed bound. For Banach algebras, we construct counter-examples to show, for example, that each component Banach algebra can fail to be Dedekind-finite while the ultraproduct is Dedekind-finite, and we explain why such a counter-example is not possible for 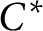 $C^*$
-algebras. Finally, the related notion of having stable rank one is also studied for ultraproducts.
$C^*$
-algebras. Finally, the related notion of having stable rank one is also studied for ultraproducts.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
Horváth acknowledges with thanks the funding received from GAČR project 19-07129Y; RVO 67985840 (Czech Republic).
References
- 1
- Cited by





