No CrossRef data available.
Article contents
Existence and symmetry breaking results for positive solutions of elliptic Hamiltonian systems
Published online by Cambridge University Press: 24 April 2024
Abstract
In this paper, we are interested in positive solutions of 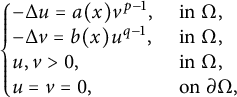 $$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = b(x)u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = b(x)u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align*} $$ $\Omega $ is a bounded annular domain (not necessarily an annulus) in
$\Omega $ is a bounded annular domain (not necessarily an annulus) in  ${\mathbb {R}}^N (N \ge 3)$ and
${\mathbb {R}}^N (N \ge 3)$ and 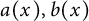 $ a(x), b(x)$ are positive continuous functions. We show the existence of a positive solution for a range of supercritical values of p and q when the problem enjoys certain mild symmetry and monotonicity conditions. We shall also address the symmetry breaking phenomena where the system is fully symmetric. Indeed, as a consequence of our results, we shall show that problem (1) has
$ a(x), b(x)$ are positive continuous functions. We show the existence of a positive solution for a range of supercritical values of p and q when the problem enjoys certain mild symmetry and monotonicity conditions. We shall also address the symmetry breaking phenomena where the system is fully symmetric. Indeed, as a consequence of our results, we shall show that problem (1) has 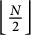 $\Bigl \lfloor \frac {N}{2} \Bigr \rfloor $ (the floor of
$\Bigl \lfloor \frac {N}{2} \Bigr \rfloor $ (the floor of  $\frac {N}{2}$) positive non-radial solutions when
$\frac {N}{2}$) positive non-radial solutions when  $ a(x)=b(x)=1$ and
$ a(x)=b(x)=1$ and  $\Omega $ is an annulus with certain assumptions on the radii. In general, for the radial case where the domain is an annulus, we prove the existence of a non-radial solution provided
$\Omega $ is an annulus with certain assumptions on the radii. In general, for the radial case where the domain is an annulus, we prove the existence of a non-radial solution provided  $$ \begin{align*}(p-1)(q-1)> \Big(1+\frac{2N}{\lambda_H}\Big)^2\left(\frac{q}{p}\right),\end{align*} $$
$$ \begin{align*}(p-1)(q-1)> \Big(1+\frac{2N}{\lambda_H}\Big)^2\left(\frac{q}{p}\right),\end{align*} $$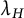 $\lambda _H$ is the best constant for the Hardy inequality on
$\lambda _H$ is the best constant for the Hardy inequality on 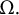 $\Omega .$ We remark that the best constant
$\Omega .$ We remark that the best constant  $\lambda _H$ for the Hardy inequality is just the characteristic of the domain, and is independent of the choices of p and
$\lambda _H$ for the Hardy inequality is just the characteristic of the domain, and is independent of the choices of p and  $q.$ For this reason, the aforementioned inequality plays a major role to prove the existence and multiplicity of non-radial solutions when the problem is fully symmetric. Our proofs use a variational formulation on appropriate convex subsets for which the lack of compactness is recovered for the supercritical problem.
$q.$ For this reason, the aforementioned inequality plays a major role to prove the existence and multiplicity of non-radial solutions when the problem is fully symmetric. Our proofs use a variational formulation on appropriate convex subsets for which the lack of compactness is recovered for the supercritical problem.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
A.M. is pleased to acknowledge the support of the National Sciences and Engineering Research Council of Canada.





