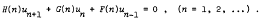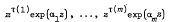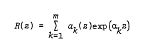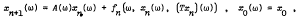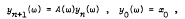Research Article
A simple model for a weak system of arithmetic
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-323
-
- Article
-
- You have access
- Export citation
Solution of a linear difference equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 325-331
-
- Article
-
- You have access
- Export citation
A note on simultaneous polynomial approximation of exponential functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 333-338
-
- Article
-
- You have access
- Export citation
Convergence and applications of reproducing kernels for classes of discrete harmonic functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 339-358
-
- Article
-
- You have access
- Export citation
A note on regular modules
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 359-364
-
- Article
-
- You have access
- Export citation
Torsionfree modules and classes of orders
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 365-371
-
- Article
-
- You have access
- Export citation
Mercer's Theorem and Fredholm resolvents
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 373-380
-
- Article
-
- You have access
- Export citation
A note on limbless trees
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 381-384
-
- Article
-
- You have access
- Export citation
On perturbed stochastic discrete systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 385-393
-
- Article
-
- You have access
- Export citation
Multifunctions of Souslin type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 395-411
-
- Article
-
- You have access
- Export citation
Regular completions of uniform convergence spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 413-424
-
- Article
-
- You have access
- Export citation
A characterization of left semiartinian rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 425-428
-
- Article
-
- You have access
- Export citation
The distribution of prime ideals of a Dedekind domain
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 429-441
-
- Article
-
- You have access
- Export citation
On equidistant sets in normed linear spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 443-454
-
- Article
-
- You have access
- Export citation
The free topological group on a cell complex
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 455-463
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
Optimum processors for some sonar detection problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 465-466
-
- Article
-
- You have access
- Export citation
Some abelian-by-nilpotent varieties of p-groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 467-469
-
- Article
-
- You have access
- Export citation
A theoretical study of the electronic structure of some organic polymers
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 470
-
- Article
-
- You have access
- Export citation
On newtonian and relativistic cosmology
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 471-472
-
- Article
-
- You have access
- Export citation
Finite generalized Hall planes and their collineation groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 473-474
-
- Article
-
- You have access
- Export citation