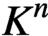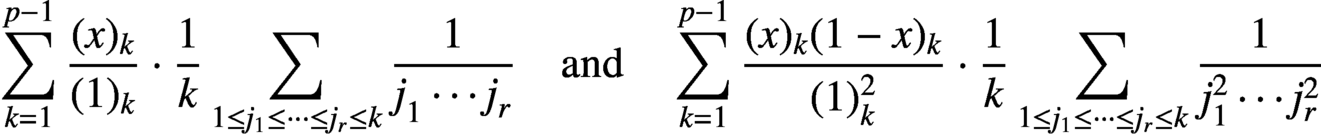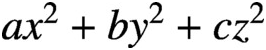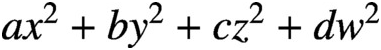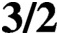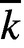Research Article
MULTINOMIAL VANDERMONDE CONVOLUTION VIA PERMANENT
- Part of:
-
- Published online by Cambridge University Press:
- 06 November 2020, pp. 353-361
-
- Article
- Export citation
THE METRIC DIMENSION OF THE ANNIHILATING-IDEAL GRAPH OF A FINITE COMMUTATIVE RING
- Part of:
-
- Published online by Cambridge University Press:
- 27 April 2021, pp. 362-368
-
- Article
- Export citation
THE NUMBER OF ROOTS OF A POLYNOMIAL SYSTEM
- Part of:
-
- Published online by Cambridge University Press:
- 09 November 2020, pp. 369-378
-
- Article
- Export citation
TWO SUPERCONGRUENCES RELATED TO MULTIPLE HARMONIC SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 28 January 2021, pp. 379-389
-
- Article
- Export citation
PRIME-UNIVERSAL DIAGONAL QUADRATIC FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2020, pp. 390-404
-
- Article
- Export citation
CONGRUENCES MODULO 4 FOR WEIGHT
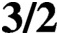 $\textbf{3/2}$
ETA-PRODUCTS
$\textbf{3/2}$
ETA-PRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2020, pp. 405-417
-
- Article
- Export citation
POINTS OF SMALL HEIGHT ON AFFINE VARIETIES DEFINED OVER FUNCTION FIELDS OF FINITE TRANSCENDENCE DEGREE
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2020, pp. 418-427
-
- Article
- Export citation
ON UNRAMIFIED SOLVABLE EXTENSIONS OF SMALL NUMBER FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 09 November 2020, pp. 428-437
-
- Article
- Export citation
SPACE OF INITIAL VALUES OF A MAP WITH A QUARTIC INVARIANT
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2020, pp. 438-449
-
- Article
- Export citation
FURTHER REMARKS ON ELEMENTARY RADICALS AND ASSOCIATED FILTERS OF IDEALS
- Part of:
-
- Published online by Cambridge University Press:
- 08 October 2020, pp. 450-460
-
- Article
- Export citation
BLOCKS WITH SMALL-DIMENSIONAL BASIC ALGEBRA
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2020, pp. 461-474
-
- Article
-
- You have access
- Open access
- Export citation
RATIONAL NEARLY SIMPLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2020, pp. 475-485
-
- Article
- Export citation
A VARIANT OF CAUCHY’S ARGUMENT PRINCIPLE FOR ANALYTIC FUNCTIONS WHICH APPLIES TO CURVES CONTAINING ZEROS
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2021, pp. 486-492
-
- Article
- Export citation
WEIGHTED COMPOSITION OPERATORS BETWEEN LORENTZ SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2020, pp. 493-505
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
EXPONENTIAL SUMS AND ADDITIVE COMBINATORICS
- Part of:
-
- Published online by Cambridge University Press:
- 09 November 2020, pp. 506-508
-
- Article
-
- You have access
- Export citation
DISTRIBUTION OF INTEGERS WITH PRESCRIBED STRUCTURE AND APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 19 October 2020, pp. 509-511
-
- Article
-
- You have access
- Export citation
INTEGRAL MEANS OF UNIVALENT FUNCTIONS ON AN ANNULUS
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2020, p. 512
-
- Article
-
- You have access
- Export citation
SOLUTIONS OF FOURTH-ORDER EVOLUTION EQUATIONS IN MATERIAL SCIENCE
- Part of:
-
- Published online by Cambridge University Press:
- 05 October 2020, pp. 513-514
-
- Article
-
- You have access
- Export citation
LINEAR RESPONSE IN DYNAMICAL SYSTEMS: OPTIMISATION AND FINITE-TIME COHERENT SETS
- Part of:
-
- Published online by Cambridge University Press:
- 09 October 2020, pp. 515-516
-
- Article
-
- You have access
- Export citation
INFLUENCE FUNCTIONS FOR DIMENSION REDUCTION METHODS
- Part of:
-
- Published online by Cambridge University Press:
- 30 October 2020, pp. 517-519
-
- Article
-
- You have access
- Export citation