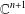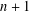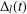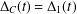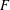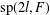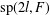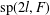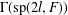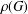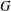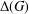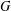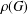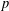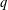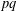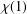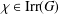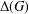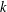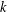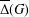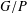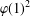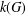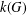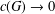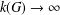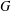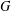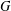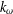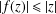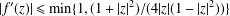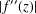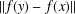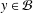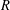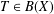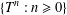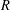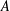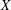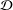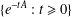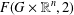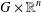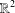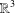Research Article
BISECTORS IN VECTOR GROUPS OVER INTEGERS
- Part of:
-
- Published online by Cambridge University Press:
- 15 August 2019, pp. 353-361
-
- Article
- Export citation
APPLICATIONS OF LERCH’S THEOREM TO PERMUTATIONS OF QUADRATIC RESIDUES
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2019, pp. 362-371
-
- Article
- Export citation
A NOTE ON MATRIX APPROXIMATION IN THE THEORY OF MULTIPLICATIVE DIOPHANTINE APPROXIMATION
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2019, pp. 372-377
-
- Article
- Export citation
POSITIVE PROPORTION OF SHORT INTERVALS CONTAINING A PRESCRIBED NUMBER OF PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 378-387
-
- Article
- Export citation
PRIMES IN ARITHMETIC PROGRESSIONS AND NONPRIMITIVE ROOTS
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2019, pp. 388-394
-
- Article
- Export citation
ON COMPLEX HOMOGENEOUS SINGULARITIES
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2019, pp. 395-409
-
- Article
- Export citation
A REMARK ON THE CHOW RING OF KÜCHLE FOURFOLDS OF TYPE
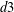 $d3$
$d3$
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2019, pp. 410-418
-
- Article
- Export citation
DIAMETER OF COMMUTING GRAPHS OF SYMPLECTIC ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 04 June 2019, pp. 419-427
-
- Article
- Export citation
ON THE REGULARITY OF CHARACTER DEGREE GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2019, pp. 428-433
-
- Article
- Export citation
MONOLITHIC BRAUER CHARACTERS
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2019, pp. 434-439
-
- Article
- Export citation
ON THE PROBABILITY DISTRIBUTION OF THE PRODUCT OF POWERS OF ELEMENTS IN COMPACT LIE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 440-445
-
- Article
- Export citation
SCHUR’S COLOURING THEOREM FOR NONCOMMUTING PAIRS
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2019, pp. 446-452
-
- Article
- Export citation
A REMARK ON THE SEPARABLE QUOTIENT PROBLEM FOR TOPOLOGICAL GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2019, pp. 453-457
-
- Article
- Export citation
ESTIMATES OF THE SECOND DERIVATIVE OF BOUNDED ANALYTIC FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2019, pp. 458-469
-
- Article
- Export citation
BOUNDARY SCHWARZ LEMMA FOR SOLUTIONS TO NONHOMOGENEOUS BIHARMONIC EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2019, pp. 470-478
-
- Article
- Export citation
ESSENTIAL AMENABILITY OF DUAL BANACH ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2019, pp. 479-488
-
- Article
- Export citation
LIPSCHITZ-TYPE INEQUALITIES FOR ANALYTIC FUNCTIONS IN BANACH ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2019, pp. 489-497
-
- Article
- Export citation
NEW COUNTEREXAMPLES ON RITT OPERATORS, SECTORIAL OPERATORS AND
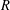 $R$-BOUNDEDNESS
$R$-BOUNDEDNESS
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2019, pp. 498-506
-
- Article
- Export citation
CATEGORY AND TOPOLOGICAL COMPLEXITY OF THE CONFIGURATION SPACE
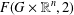 $F(G\times \mathbb{R}^{n},2)$
$F(G\times \mathbb{R}^{n},2)$
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2019, pp. 507-517
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
WEAK SUBORDINATION OF MULTIVARIATE LÉVY PROCESSES
- Part of:
-
- Published online by Cambridge University Press:
- 09 July 2019, pp. 518-519
-
- Article
-
- You have access
- Export citation