Hostname: page-component-848d4c4894-2xdlg Total loading time: 0 Render date: 2024-06-27T17:22:35.432Z Has data issue: false hasContentIssue false
  • English
  • Français

The skeleton of a variety of groups

Published online by Cambridge University Press:  17 April 2009

R.M. Bryant  and
L.G. Kovács
R.M. Bryant
Affiliation:
Department of Mathematics, Institute of Advanced Studies, Australian National University, Canberra, ACT.
L.G. Kovács
Affiliation:
Department of Mathematics, Institute of Advanced Studies, Australian National University, Canberra, ACT.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The skeleton 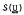of a variety 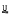of groups is defined to be the intersection of the section closed classes of groups which generate 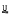. If m is an integer, m > 1, 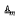is the variety of all abelian groups of exponent dividing m, and 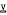, is any locally finite variety, it is shown that the skeleton of the product variety 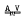is the section closure of the class of finite monolithic groups in 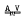. In particular, S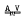) generates 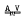. The elements of S 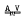are described more explicitly and as a consequence it is shown that S 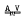consists of all finite groups in 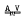if and only if m is a power of some prime p and the centre of the countably infinite relatively free group of 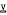, is a p–group.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 6 , Issue 3 , June 1972 , pp. 357 - 378
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Brisley, Warren and Kovács, L.G., “On soluble groups of prime-power exponent”, Bull. Austral. Math. Soc. 4 (1971), 389–396.CrossRefGoogle Scholar
[2]Bryant, R.M. and Kovács, L.G., “Tensor products of representations of finite groups”, (to appear).Google Scholar
[3]Cossey, P.J., “On varieties of A-groups”, Ph.D. thesis, Australian National University, 1966.Google Scholar
[4]Cossey, John, “Critical groups and the lattice of varieties”, Proc. Amer. Math. Soc. 20 (1969), 217–221.CrossRefGoogle Scholar
[5]Curtis, Charles W.; Reiner, Irving, Representation theory of finite groups and associative algebras (Pure and Applied Mathematics, XI. Interscience [John Wiley & Sons], New York, London, 1962).Google Scholar
[6]Fein, Burton, “Representations of direct products of finite groups”, Pacific J. Math. 20 (1967), 45–58.CrossRefGoogle Scholar
[7]Huppert, B., Endliche Gruppen I (Die Grundlehren der mathematischen Wissenschaften, Band 134. Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar
[8]Kovács, L.G. and Newman, M.F., “On critical groups”, J. Austral. Math. Soc. 6 (1966), 237–250.CrossRefGoogle Scholar
[9]Neumann, Hanna, Varieties of groups (Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 37. Springer-Verlag, Berlin, Heidelberg, New York, 1967).CrossRefGoogle Scholar