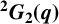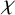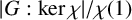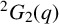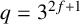1 Introduction
Let G be a finite group and
![]() $\mbox {Irr}(G)$
be the set of all irreducible complex characters of G. The concept of codegrees was introduced by Chillag and Herzog in [Reference Chillag and Herzog6], where the codegree of
$\mbox {Irr}(G)$
be the set of all irreducible complex characters of G. The concept of codegrees was introduced by Chillag and Herzog in [Reference Chillag and Herzog6], where the codegree of
![]() $\chi $
was defined as
$\chi $
was defined as
![]() ${|G|}/{\chi (1)}$
for a character
${|G|}/{\chi (1)}$
for a character
![]() $\chi \in \mbox {Irr}(G)$
. The definition was modified to
$\chi \in \mbox {Irr}(G)$
. The definition was modified to
![]() $ {\mathrm{cod}}(\,\chi )={|G:\ker (\,\chi )|}/{\chi (1)}$
by Qian et al. in [Reference Qian, Wang and Wei18] so that there is no different meaning for
$ {\mathrm{cod}}(\,\chi )={|G:\ker (\,\chi )|}/{\chi (1)}$
by Qian et al. in [Reference Qian, Wang and Wei18] so that there is no different meaning for
![]() $ {\mathrm{cod}}(\,\chi )$
when
$ {\mathrm{cod}}(\,\chi )$
when
![]() $\chi $
is considered as a character in some quotient group of G. Because the relationship between codegrees and degrees is very close, we may expect to characterise the structure of groups by codegrees. During the past few years, the study of character codegrees has been very active and many results have been obtained, including the relationship between codegrees and element orders, codegrees of p-groups and groups with few codegrees (see, for example, [Reference Alizadeh, Behravesh, Ghaffarzadeh, Ghasemi and Hekmatarah2, Reference Du and Lewis8, Reference Isaacs11, Reference Liu and Yang14, Reference Liu and Yang15, Reference Qian17]).
$\chi $
is considered as a character in some quotient group of G. Because the relationship between codegrees and degrees is very close, we may expect to characterise the structure of groups by codegrees. During the past few years, the study of character codegrees has been very active and many results have been obtained, including the relationship between codegrees and element orders, codegrees of p-groups and groups with few codegrees (see, for example, [Reference Alizadeh, Behravesh, Ghaffarzadeh, Ghasemi and Hekmatarah2, Reference Du and Lewis8, Reference Isaacs11, Reference Liu and Yang14, Reference Liu and Yang15, Reference Qian17]).
Let cd
![]() $(G) = \{\,\chi (1) \ |\ \chi \in \mbox {Irr}(G)\}$
. Huppert made the following conjecture (which has been verified for sporadic simple groups, alternating groups and some simple groups of Lie type with low rank).
$(G) = \{\,\chi (1) \ |\ \chi \in \mbox {Irr}(G)\}$
. Huppert made the following conjecture (which has been verified for sporadic simple groups, alternating groups and some simple groups of Lie type with low rank).
Huppert’s Conjecture: Let H be any finite nonabelian simple group and G a finite group such that cd
![]() $(G)$
= cd
$(G)$
= cd
![]() $(H)$
. Then
$(H)$
. Then
![]() $G \cong H \times A$
, where A is abelian.
$G \cong H \times A$
, where A is abelian.
We denote cod
![]() $(G) = \{ {\mathrm{cod}}(\,\chi ) \ |\ \chi \in \mbox {Irr}(G)\}$
. Qian made the following conjecture (Question 20.79 in the Kourovka Notebook [Reference Khukhro12]).
$(G) = \{ {\mathrm{cod}}(\,\chi ) \ |\ \chi \in \mbox {Irr}(G)\}$
. Qian made the following conjecture (Question 20.79 in the Kourovka Notebook [Reference Khukhro12]).
Codegree version of Huppert’s conjecture: Let H be any finite nonabelian simple group and G a finite group such that
![]() $ {\mathrm{cod}}(G)= {\mathrm{cod}}(H)$
. Then
$ {\mathrm{cod}}(G)= {\mathrm{cod}}(H)$
. Then
![]() $G\cong H$
.
$G\cong H$
.
This conjecture was shown to hold for
![]() $ {\mathrm{PSL}}(2,q)$
in [Reference Bahri, Akhlaghi and Khosravi4]. In [Reference Ahanjideh1], the conjecture was proven for
$ {\mathrm{PSL}}(2,q)$
in [Reference Bahri, Akhlaghi and Khosravi4]. In [Reference Ahanjideh1], the conjecture was proven for
![]() ${}^2B_2(2^{2f+1})$
, where
${}^2B_2(2^{2f+1})$
, where
![]() $f \ge 1$
,
$f \ge 1$
,
![]() $ {\mathrm{PSL}}(3,4)$
,
$ {\mathrm{PSL}}(3,4)$
,
![]() ${\operatorname {Alt}}_7$
and
${\operatorname {Alt}}_7$
and
![]() $J_1$
. The conjecture also holds in the cases where H is
$J_1$
. The conjecture also holds in the cases where H is
![]() $M_{11}, M_{12}, M_{22}, M_{23}$
or
$M_{11}, M_{12}, M_{22}, M_{23}$
or
![]() $ {\mathrm{PSL}}(3,3)$
by [Reference Gintz, Kortje, Laurence, Liu, Wang and Yang9]. For
$ {\mathrm{PSL}}(3,3)$
by [Reference Gintz, Kortje, Laurence, Liu, Wang and Yang9]. For
![]() $ {\mathrm{PSL}}(3,q)$
and
$ {\mathrm{PSL}}(3,q)$
and
![]() $ {\mathrm{PSU}}(3,q)$
, the conjecture was confirmed in [Reference Liu and Yang16]. In this paper, we continue the study of the conjecture and establish the following result.
$ {\mathrm{PSU}}(3,q)$
, the conjecture was confirmed in [Reference Liu and Yang16]. In this paper, we continue the study of the conjecture and establish the following result.
Theorem 1.1. If H is isomorphic to a simple Ree group
![]() ${}^2G_2(3^{2f+1}), f\geq 1$
and G is a finite group such that
${}^2G_2(3^{2f+1}), f\geq 1$
and G is a finite group such that
![]() $ {\mathrm{cod}}(G)= {\mathrm{cod}}(H)$
, then
$ {\mathrm{cod}}(G)= {\mathrm{cod}}(H)$
, then
![]() $G\cong H$
.
$G\cong H$
.
2 Preliminary results
First, we give a list of simple groups with few codegrees. The cases for finite groups G with
![]() $| {\mathrm{cod}}(G)| \le 3$
are studied in [Reference Alizadeh, Behravesh, Ghaffarzadeh, Ghasemi and Hekmatarah2]. In particular, those groups are all solvable.
$| {\mathrm{cod}}(G)| \le 3$
are studied in [Reference Alizadeh, Behravesh, Ghaffarzadeh, Ghasemi and Hekmatarah2]. In particular, those groups are all solvable.
Lemma 2.1. Let G be a nonabelian finite simple group. If
![]() $|\mathrm{cod}(G)| \leq 11$
, then one of the following holds:
$|\mathrm{cod}(G)| \leq 11$
, then one of the following holds:
-
(a)
 $| {\mathrm{cod}}(G)|=4$
and
$| {\mathrm{cod}}(G)|=4$
and
 $G= { {\mathrm{PSL}}}(2,2^f)$
for
$G= { {\mathrm{PSL}}}(2,2^f)$
for
 $f\geq 2$
;
$f\geq 2$
; -
(b)
 $| {\mathrm{cod}}(G)|=5$
and
$| {\mathrm{cod}}(G)|=5$
and
 $G= { {\mathrm{PSL}}}(2,p^f)$
,
$G= { {\mathrm{PSL}}}(2,p^f)$
,
 $p\neq 2, p^f>5$
;
$p\neq 2, p^f>5$
; -
(c)
 $| {\mathrm{cod}}(G)|=6$
and
$| {\mathrm{cod}}(G)|=6$
and
 $G= {}^2B_2(2^{2f+1})$
,
$G= {}^2B_2(2^{2f+1})$
,
 $f\geq 1$
, or
$f\geq 1$
, or
 $G= { {\mathrm{PSL}}}(3,4)$
;
$G= { {\mathrm{PSL}}}(3,4)$
; -
(d)
 $| {\mathrm{cod}}(G)|=7$
and
$| {\mathrm{cod}}(G)|=7$
and
 $G= { {\mathrm{PSL}}}(3,3), {\operatorname {Alt}}_7, M_{11}$
or
$G= { {\mathrm{PSL}}}(3,3), {\operatorname {Alt}}_7, M_{11}$
or
 $J_1$
;
$J_1$
; -
(e)
 $| {\mathrm{cod}}(G)|=8$
and
$| {\mathrm{cod}}(G)|=8$
and
 $G= { {\mathrm{PSL}}}(3,q)$
, where
$G= { {\mathrm{PSL}}}(3,q)$
, where
 $4< q\not \equiv 1\ (\bmod \ 3)$
, or
$4< q\not \equiv 1\ (\bmod \ 3)$
, or
 $G = {\mathrm{PSU}}(3,q)$
, where
$G = {\mathrm{PSU}}(3,q)$
, where
 $4 < q \not \equiv -1\ (\bmod \ 3)$
, or
$4 < q \not \equiv -1\ (\bmod \ 3)$
, or
 $G=G_2(2)'$
;
$G=G_2(2)'$
; -
(f)
 $| {\mathrm{cod}}(G)|=9$
and
$| {\mathrm{cod}}(G)|=9$
and
 $G= { {\mathrm{PSL}}}(3,q)$
, where
$G= { {\mathrm{PSL}}}(3,q)$
, where
 $4<q\equiv 1\ (\bmod \ 3)$
, or
$4<q\equiv 1\ (\bmod \ 3)$
, or
 $G= {\mathrm{PSU}}(3,q)$
, where
$G= {\mathrm{PSU}}(3,q)$
, where
 $4<q \equiv -1\ (\bmod \ 3)$
;
$4<q \equiv -1\ (\bmod \ 3)$
; -
(g)
 $| {\mathrm{cod}}(G)|=10$
and
$| {\mathrm{cod}}(G)|=10$
and
 $G= M_{22}$
;
$G= M_{22}$
; -
(h)
 $| {\mathrm{cod}}(G)|=11$
and
$| {\mathrm{cod}}(G)|=11$
and
 $G= { {\mathrm{PSL}}}(4,2), M_{12}, M_{23}$
or
$G= { {\mathrm{PSL}}}(4,2), M_{12}, M_{23}$
or
 ${}^2G_2(3^{2f+1}), f\geq 1$
.
${}^2G_2(3^{2f+1}), f\geq 1$
.
Proof. For a simple group G, each nontrivial irreducible character is faithful. Then
![]() $| {\mathrm{cod}}(G)|=| {\mbox {cd}}(G)|$
and the result follows from [Reference Aziziheris, Shafiei and Shirjian3, Theorem 1.1].
$| {\mathrm{cod}}(G)|=| {\mbox {cd}}(G)|$
and the result follows from [Reference Aziziheris, Shafiei and Shirjian3, Theorem 1.1].
The character degree sets for the relevant simple groups have been worked out. Using the definition of codegrees and the fact that the kernel of a nontrivial character is trivial, it is easy to calculate the codegrees. We list the relevant codegree sets in Table 1 for easy reference. Please see [Reference Ahanjideh1, Reference Bahri, Akhlaghi and Khosravi4, Reference Conway, Curtis, Norton, Parker and Wilson7, Reference Simpson and Frame19–Reference Ward21] for the details.
Table 1 Codegree sets for some simple groups.

Lemma 2.2. If a simple group G is isomorphic to
![]() $ {\mathrm{PSL}}(2,k)$
,
$ {\mathrm{PSL}}(2,k)$
,
![]() ${}^2B_2(q^2)$
,
${}^2B_2(q^2)$
,
![]() $ {\mathrm{PSL}}(3,4)$
,
$ {\mathrm{PSL}}(3,4)$
,
![]() ${\operatorname {Alt}}_7$
,
${\operatorname {Alt}}_7$
,
![]() $J_1$
,
$J_1$
,
![]() $M_{11}$
,
$M_{11}$
,
![]() $ {\mathrm{PSL}}(3,3)$
,
$ {\mathrm{PSL}}(3,3)$
,
![]() $G_2(2)'$
,
$G_2(2)'$
,
![]() $M_{22}$
,
$M_{22}$
,
![]() $ {\mathrm{PSL}}(4,2)$
,
$ {\mathrm{PSL}}(4,2)$
,
![]() $M_{12}$
,
$M_{12}$
,
![]() $M_{23}$
,
$M_{23}$
,
![]() $ {\mathrm{PSL}}(3,q)$
,
$ {\mathrm{PSL}}(3,q)$
,
![]() $ {\mathrm{PSU}}(3,q)$
or
$ {\mathrm{PSU}}(3,q)$
or
![]() ${}^2G_2(q)$
, then
${}^2G_2(q)$
, then
![]() $ {\mathrm{cod}}(G)$
can be found in Table 1.
$ {\mathrm{cod}}(G)$
can be found in Table 1.
To end this section, we state a result about the maximal subgroups of
![]() ${}^2G_2(3^{2f+1})$
,
${}^2G_2(3^{2f+1})$
,
![]() $f\geq 1$
. This is obtained from [Reference Kleidman13, Theorem C].
$f\geq 1$
. This is obtained from [Reference Kleidman13, Theorem C].
Lemma 2.3. Let K be a maximal subgroup of
![]() $\mathrm {}^2G_2(q)$
, where
$\mathrm {}^2G_2(q)$
, where
![]() $q=3^{2f+1}$
,
$q=3^{2f+1}$
,
![]() $f \geq 1$
. Then K is isomorphic to one of the groups in Table 2.
$f \geq 1$
. Then K is isomorphic to one of the groups in Table 2.
Table 2 Maximal subgroups of
![]() $\mathrm {}^2G_2(q)$
,
$\mathrm {}^2G_2(q)$
,
![]() $q \geq 27$
.
$q \geq 27$
.

3 Main result for
 ${}^2G_2(3^{2f+1})$
${}^2G_2(3^{2f+1})$
Sometimes it is convenient to consider the ratio of a set. Let A be a set of nonzero integers. We define
![]() $\operatorname {ratio}(A)=\{a/b \ | \ a, b \in A, a \ne b$
and
$\operatorname {ratio}(A)=\{a/b \ | \ a, b \in A, a \ne b$
and
![]() $b \ne 1\}$
.
$b \ne 1\}$
.
Lemma 3.1. Let G be a finite group with
![]() $ {\mathrm{cod}}(G)= {\mathrm{cod}}({}^2G_2(3^{2f+1}))$
, where
$ {\mathrm{cod}}(G)= {\mathrm{cod}}({}^2G_2(3^{2f+1}))$
, where
![]() $f \geq 1$
. If N is a maximal normal subgroup of G, then
$f \geq 1$
. If N is a maximal normal subgroup of G, then
![]() $G/N \cong {}^2G_2(3^{2f+1})$
.
$G/N \cong {}^2G_2(3^{2f+1})$
.
Proof. Let N be a maximal normal subgroup of G. We set
![]() $q=3^{2f+1}$
. Since
$q=3^{2f+1}$
. Since
![]() $ {\mathrm{cod}}(G)= {\mathrm{cod}}({}^2G_2(q))$
, we see that G is perfect. Then
$ {\mathrm{cod}}(G)= {\mathrm{cod}}({}^2G_2(q))$
, we see that G is perfect. Then
![]() $G/N$
is a nonabelian simple group. Since
$G/N$
is a nonabelian simple group. Since
![]() $ {\mathrm{cod}}(G/N)\subseteq {\mathrm{cod}}(G)$
, we see that
$ {\mathrm{cod}}(G/N)\subseteq {\mathrm{cod}}(G)$
, we see that
![]() $| {\mathrm{cod}}(G/N)|$
is either
$| {\mathrm{cod}}(G/N)|$
is either
![]() $4, 5, 6, 7, 8, 9, 10$
or
$4, 5, 6, 7, 8, 9, 10$
or
![]() $11$
.
$11$
.
Suppose
![]() $| {\mbox {cod}}(G/N)| = 4$
. Then
$| {\mbox {cod}}(G/N)| = 4$
. Then
![]() $G/N\cong {\mbox {PSL}}(2,k)$
, where
$G/N\cong {\mbox {PSL}}(2,k)$
, where
![]() $k=2^t \geq 4$
, and
$k=2^t \geq 4$
, and
![]() $ {\mbox {cod}}(G/N)=\{1, k(k-1), k(k+1), k^2-1\}$
. Since
$ {\mbox {cod}}(G/N)=\{1, k(k-1), k(k+1), k^2-1\}$
. Since
![]() $k^2-1$
is the only nontrivial odd codegree, it must be the same as either
$k^2-1$
is the only nontrivial odd codegree, it must be the same as either
![]() $3^{5f+3}(q^2- q + 1)$
or
$3^{5f+3}(q^2- q + 1)$
or
![]() $q^3( q+1-3m)$
or
$q^3( q+1-3m)$
or
![]() $q^3(q +1 + 3m )$
. Note that
$q^3(q +1 + 3m )$
. Note that
![]() $(k+1,k-1)=1$
. Suppose that
$(k+1,k-1)=1$
. Suppose that
![]() $k^2-1 = 3^{5f+3} (q^2- q + 1)$
. If
$k^2-1 = 3^{5f+3} (q^2- q + 1)$
. If
![]() $3^{5f+3} | k-1$
, then
$3^{5f+3} | k-1$
, then
![]() $k+1 | q^2-q+1$
. Clearly
$k+1 | q^2-q+1$
. Clearly
![]() $q^2-q+1 < 3^{5f+3}$
, which implies that
$q^2-q+1 < 3^{5f+3}$
, which implies that
![]() $ k+1 < k-1$
, which is a contradiction. If
$ k+1 < k-1$
, which is a contradiction. If
![]() $ 3^{5f+3} | k+1$
, then
$ 3^{5f+3} | k+1$
, then
![]() $ k-1 | q^2-q+1$
. Clearly
$ k-1 | q^2-q+1$
. Clearly
![]() $ 3^{5f+3} - (q^2-q+1) = 3^{5f+3}-3^{4f+2}+ 3^{2f+1}-1> 2$
, which implies that
$ 3^{5f+3} - (q^2-q+1) = 3^{5f+3}-3^{4f+2}+ 3^{2f+1}-1> 2$
, which implies that
![]() $ (k+1)- (k-1)> 2$
, which is a contradiction. Suppose
$ (k+1)- (k-1)> 2$
, which is a contradiction. Suppose
![]() $k^2-1 = q^3( q+1-3m)$
. If
$k^2-1 = q^3( q+1-3m)$
. If
![]() $q^3 | k-1$
, then
$q^3 | k-1$
, then
![]() $k+1 | ( q+1-3m)$
. Obviously, we have
$k+1 | ( q+1-3m)$
. Obviously, we have
![]() $q^3> q+1-3m$
, which implies that
$q^3> q+1-3m$
, which implies that
![]() $k-1> k+1$
, which is a contradiction. If
$k-1> k+1$
, which is a contradiction. If
![]() $q^3 | k+1$
, then
$q^3 | k+1$
, then
![]() $k-1 | ( q+1-3m)$
. Clearly
$k-1 | ( q+1-3m)$
. Clearly
![]() $q^3 - (q+1-3m) = (3^{6f+3}- 3^{2f+1}-1 ) + 3^{f+1}> 2$
, which implies that
$q^3 - (q+1-3m) = (3^{6f+3}- 3^{2f+1}-1 ) + 3^{f+1}> 2$
, which implies that
![]() $k+1 - (k-1)> 2$
, which is a contradiction. Suppose
$k+1 - (k-1)> 2$
, which is a contradiction. Suppose
![]() $k^2-1 = q^3 (q+1+3m)$
. If
$k^2-1 = q^3 (q+1+3m)$
. If
![]() $q^3 | k-1$
, then
$q^3 | k-1$
, then
![]() $k+1 | ( q+1+3m)$
. Since
$k+1 | ( q+1+3m)$
. Since
![]() $q^3> q+1+3m$
, we have
$q^3> q+1+3m$
, we have
![]() $k-1> k+1$
, which is a contradiction. If
$k-1> k+1$
, which is a contradiction. If
![]() $q^3 | k+1$
, then
$q^3 | k+1$
, then
![]() $k-1 | ( q+1+3m)$
. Clearly
$k-1 | ( q+1+3m)$
. Clearly
![]() $q^3 - (q+1+3m) = 3^{6f+3}-( 3^{2f+1}+1 + 3^{f+1} )> 2$
, which implies that
$q^3 - (q+1+3m) = 3^{6f+3}-( 3^{2f+1}+1 + 3^{f+1} )> 2$
, which implies that
![]() $k+1 - (k-1)> 2$
, which is a contradiction.
$k+1 - (k-1)> 2$
, which is a contradiction.
Suppose
![]() $| {\mathrm{cod}}(G/N)|=5$
. Then
$| {\mathrm{cod}}(G/N)|=5$
. Then
![]() $G/N \cong {\mathrm{PSL}}(2,k)$
, where
$G/N \cong {\mathrm{PSL}}(2,k)$
, where
![]() $k>5$
is an odd prime power. We note that
$k>5$
is an odd prime power. We note that
![]() $2 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
$2 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
![]() $\operatorname {ratio}( {\mathrm{cod}}(G))$
is
$\operatorname {ratio}( {\mathrm{cod}}(G))$
is
![]() $q- 1$
, where
$q- 1$
, where
![]() $q \geq 27$
.
$q \geq 27$
.
Suppose
![]() $| {\mathrm{cod}}(G/N)| =6$
. Then
$| {\mathrm{cod}}(G/N)| =6$
. Then
![]() $G/N \cong {}^2B_2(2^{2t+1}) $
or
$G/N \cong {}^2B_2(2^{2t+1}) $
or
![]() $ {\mathrm{PSL}}(3,4) $
.
$ {\mathrm{PSL}}(3,4) $
.
Suppose
![]() $G/N \cong {}^2B_2(s)$
with
$G/N \cong {}^2B_2(s)$
with
![]() $s=2^{2t+1}$
and
$s=2^{2t+1}$
and
![]() $r=2^t$
,
$r=2^t$
,
![]() $t \ge 1$
. The only nontrivial odd codegree in
$t \ge 1$
. The only nontrivial odd codegree in
![]() $ {\mathrm{cod}}({}^2B_2(s))$
is
$ {\mathrm{cod}}({}^2B_2(s))$
is
![]() $(s - 1)(s^2 + 1)$
. Thus,
$(s - 1)(s^2 + 1)$
. Thus,
![]() $(s - 1)(s^2 + 1)$
could be equal to either
$(s - 1)(s^2 + 1)$
could be equal to either
![]() $3^{5f+3} (q^2- q + 1)$
,
$3^{5f+3} (q^2- q + 1)$
,
![]() $q^3( q+1-3m)$
or
$q^3( q+1-3m)$
or
![]() $q^3(q +1 + 3m )$
. Note that
$q^3(q +1 + 3m )$
. Note that
![]() ${(s - 1 , s^2 + 1) =1}$
. Suppose
${(s - 1 , s^2 + 1) =1}$
. Suppose
![]() $(s - 1)(s^2 + 1) = 3^{5f+3} (q^2- q + 1)$
. If
$(s - 1)(s^2 + 1) = 3^{5f+3} (q^2- q + 1)$
. If
![]() $3^{5f+3} | s-1$
, then
$3^{5f+3} | s-1$
, then
![]() $s^2 + 1 | q^2- q + 1$
. Clearly
$s^2 + 1 | q^2- q + 1$
. Clearly
![]() $3^{5f+3}> q^2-q+1$
, which implies that
$3^{5f+3}> q^2-q+1$
, which implies that
![]() $s-1> s^2+1$
, which is a contradiction. If
$s-1> s^2+1$
, which is a contradiction. If
![]() $3^{5f+3} | s^2+1$
, we have a contradiction since
$3^{5f+3} | s^2+1$
, we have a contradiction since
![]() $s^2-1$
is divisible by 3. Suppose
$s^2-1$
is divisible by 3. Suppose
![]() $(s - 1) (s^2 + 1) = q^3 (q + 1 - 3m)$
. If
$(s - 1) (s^2 + 1) = q^3 (q + 1 - 3m)$
. If
![]() $q^3 | s-1$
, then
$q^3 | s-1$
, then
![]() $ s^2 +1 | q+1-3m$
. Clearly
$ s^2 +1 | q+1-3m$
. Clearly
![]() $q^3> q+1-3m$
, which implies that
$q^3> q+1-3m$
, which implies that
![]() $s-1> s^2+1$
, which is a contradiction. If
$s-1> s^2+1$
, which is a contradiction. If
![]() $q^3 | s^2+1$
, then
$q^3 | s^2+1$
, then
![]() $s-1 | q+1-3m$
. This implies that
$s-1 | q+1-3m$
. This implies that
![]() $q^3 \leq (q+2-3m)^2+1$
, which is a contradiction. Suppose
$q^3 \leq (q+2-3m)^2+1$
, which is a contradiction. Suppose
![]() $(s - 1)(s^2 + 1) = q^3 (q + 1 + 3m)$
. If
$(s - 1)(s^2 + 1) = q^3 (q + 1 + 3m)$
. If
![]() $q^3 | s-1$
, then
$q^3 | s-1$
, then
![]() $s^2 +1 | q+1+3m$
. Clearly
$s^2 +1 | q+1+3m$
. Clearly
![]() $q^3> q+1+3m$
, which implies that
$q^3> q+1+3m$
, which implies that
![]() $s-1> s^2+1$
, which is a contradiction. If
$s-1> s^2+1$
, which is a contradiction. If
![]() $q^3 | s^2+1$
, then
$q^3 | s^2+1$
, then
![]() $s-1 | q+1+3m$
. This implies that
$s-1 | q+1+3m$
. This implies that
![]() $q^3 \leq (q+2+3m)^2 + 1$
, which is a contradiction.
$q^3 \leq (q+2+3m)^2 + 1$
, which is a contradiction.
Suppose
![]() $G/N \cong {\mathrm{PSL}}(3,4)$
. Note that
$G/N \cong {\mathrm{PSL}}(3,4)$
. Note that
![]() $3^2{\cdot } 5{\cdot } 7$
is the only nontrivial odd codegree in
$3^2{\cdot } 5{\cdot } 7$
is the only nontrivial odd codegree in
![]() $ {\mathrm{cod}}(G/N)$
. Thus,
$ {\mathrm{cod}}(G/N)$
. Thus,
![]() $3^2{\cdot } 5{\cdot } 7$
could be equal to either
$3^2{\cdot } 5{\cdot } 7$
could be equal to either
![]() $3^{5f+3} (q^2- q + 1)$
,
$3^{5f+3} (q^2- q + 1)$
,
![]() $q^3( q+1-3m)$
or
$q^3( q+1-3m)$
or
![]() $q^3(q +1 + 3m )$
. By considering the power of
$q^3(q +1 + 3m )$
. By considering the power of
![]() $3$
in those numbers, we see that each is impossible.
$3$
in those numbers, we see that each is impossible.
Suppose
![]() $| {\mathrm{cod}}(G/N)| = 7$
. Then
$| {\mathrm{cod}}(G/N)| = 7$
. Then
![]() $G/N \cong {\mathrm{PSL}}(3,3)$
,
$G/N \cong {\mathrm{PSL}}(3,3)$
,
![]() ${\operatorname {Alt}}_7$
,
${\operatorname {Alt}}_7$
,
![]() $M_{11}$
or
$M_{11}$
or
![]() $J_1$
.
$J_1$
.
Suppose
![]() $G/N \cong {\mathrm{PSL}}(3,3)$
. Note that
$G/N \cong {\mathrm{PSL}}(3,3)$
. Note that
![]() $3 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
$3 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
![]() $\operatorname {ratio}( {\mathrm{cod}}(G))$
is
$\operatorname {ratio}( {\mathrm{cod}}(G))$
is
![]() $q- 1$
, where
$q- 1$
, where
![]() $q \geq 27$
.
$q \geq 27$
.
Suppose
![]() $G/N \cong {\operatorname {Alt}}_7$
. Then
$G/N \cong {\operatorname {Alt}}_7$
. Then
![]() $2^3 {\cdot } 3^2 \in {\mathrm{cod}}(G/N)$
. Since the powers of
$2^3 {\cdot } 3^2 \in {\mathrm{cod}}(G/N)$
. Since the powers of
![]() $3$
of all the terms that are divisible by
$3$
of all the terms that are divisible by
![]() $3$
in
$3$
in
![]() $ {\mathrm{cod}}(G)$
are greater than
$ {\mathrm{cod}}(G)$
are greater than
![]() $2$
, this is a contradiction.
$2$
, this is a contradiction.
Suppose
![]() $G/N \cong M_{11}$
. Note that
$G/N \cong M_{11}$
. Note that
![]() $5 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
$5 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
![]() $\operatorname {ratio}( {\mathrm{cod}}(G))$
is
$\operatorname {ratio}( {\mathrm{cod}}(G))$
is
![]() $q- 1$
, where
$q- 1$
, where
![]() $q \geq 27$
.
$q \geq 27$
.
Suppose
![]() $G/N \cong J_1$
. Note that
$G/N \cong J_1$
. Note that
![]() $ {\mathrm{cod}}(J_1)$
has two nontrivial odd codegrees
$ {\mathrm{cod}}(J_1)$
has two nontrivial odd codegrees
![]() $7{\cdot } 11{\cdot } 19$
and
$7{\cdot } 11{\cdot } 19$
and
![]() $3{\cdot } 5{\cdot } 11{\cdot } 19$
. The odd codegrees in
$3{\cdot } 5{\cdot } 11{\cdot } 19$
. The odd codegrees in
![]() $ {\mathrm{cod}}(G)$
are
$ {\mathrm{cod}}(G)$
are
![]() $3^{5f+3}(q^2-q+1)$
,
$3^{5f+3}(q^2-q+1)$
,
![]() $q^3 ( q+1 - 3m)$
and
$q^3 ( q+1 - 3m)$
and
![]() $q^3 ( q+1 + 3m)$
. By considering the power of
$q^3 ( q+1 + 3m)$
. By considering the power of
![]() $3$
in those numbers, we see that each is impossible.
$3$
in those numbers, we see that each is impossible.
Suppose
![]() $| {\mathrm{cod}}(G/N)|=8$
. Then
$| {\mathrm{cod}}(G/N)|=8$
. Then
![]() $G/N \cong { {\mathrm{PSL}}}(3,s)$
, where
$G/N \cong { {\mathrm{PSL}}}(3,s)$
, where
![]() $4< s\not \equiv 1\ (\bmod \ 3)$
,
$4< s\not \equiv 1\ (\bmod \ 3)$
,
![]() $ {\mathrm{PSU}}(3,s)$
, where
$ {\mathrm{PSU}}(3,s)$
, where
![]() $4 < s \not \equiv -1\ (\bmod \ 3)$
, or
$4 < s \not \equiv -1\ (\bmod \ 3)$
, or
![]() $G_2(2)'$
.
$G_2(2)'$
.
Suppose
![]() $ {\mathrm{cod}}(G/N) = {\mathrm{cod}}( {\mathrm{PSU}}(3,s))$
with
$ {\mathrm{cod}}(G/N) = {\mathrm{cod}}( {\mathrm{PSU}}(3,s))$
with
![]() $4 < s \not \equiv -1\ (\bmod \ 3)$
. Note that
$4 < s \not \equiv -1\ (\bmod \ 3)$
. Note that
![]() $3 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
$3 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
![]() $\operatorname {ratio}( {\mathrm{cod}}(G))$
is
$\operatorname {ratio}( {\mathrm{cod}}(G))$
is
![]() $q- 1$
, where
$q- 1$
, where
![]() $q \geq 27$
.
$q \geq 27$
.
Suppose
![]() $G/N \cong G_2(2)'$
. Note that
$G/N \cong G_2(2)'$
. Note that
![]() $3 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
$3 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
![]() $\operatorname {ratio}( {\mathrm{cod}}(G))$
is
$\operatorname {ratio}( {\mathrm{cod}}(G))$
is
![]() $q- 1$
, where
$q- 1$
, where
![]() $q \geq 27$
.
$q \geq 27$
.
Suppose
![]() $G/N \cong {\mathrm{PSL}}(3,s)$
for some
$G/N \cong {\mathrm{PSL}}(3,s)$
for some
![]() $4 < s \not \equiv 1\ (\bmod \ 3)$
. Note that
$4 < s \not \equiv 1\ (\bmod \ 3)$
. Note that
![]() $s-1, s+1 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
, and the only nontrivial integers in
$s-1, s+1 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
, and the only nontrivial integers in
![]() $\operatorname {ratio}( {\mathrm{cod}}(G))$
are
$\operatorname {ratio}( {\mathrm{cod}}(G))$
are
![]() $q-1$
, q,
$q-1$
, q,
![]() $q+1$
, where q is a power of
$q+1$
, where q is a power of
![]() $3$
and
$3$
and
![]() $q \geq 27$
. This will force
$q \geq 27$
. This will force
![]() $s=q$
, which is a contradiction since
$s=q$
, which is a contradiction since
![]() $q^3(q-1)^2 \not \in {\mathrm{cod}}(G)$
.
$q^3(q-1)^2 \not \in {\mathrm{cod}}(G)$
.
Suppose
![]() $| {\mathrm{cod}}(G/N)| = 9$
. Then
$| {\mathrm{cod}}(G/N)| = 9$
. Then
![]() $G/N \cong { {\mathrm{PSL}}}(3,s)$
, where
$G/N \cong { {\mathrm{PSL}}}(3,s)$
, where
![]() $4<s\equiv 1\ (\bmod \ 3)$
, or
$4<s\equiv 1\ (\bmod \ 3)$
, or
![]() $ {\mathrm{PSU}}(3,s)$
, where
$ {\mathrm{PSU}}(3,s)$
, where
![]() $4<s \equiv -1\ (\bmod \ 3)$
.
$4<s \equiv -1\ (\bmod \ 3)$
.
Suppose
![]() $G/N \cong {\mathrm{PSL}}(3, s)$
with
$G/N \cong {\mathrm{PSL}}(3, s)$
with
![]() $4 < s\equiv 1\ (\bmod \ 3)$
. Note that
$4 < s\equiv 1\ (\bmod \ 3)$
. Note that
![]() $3 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
$3 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
![]() $\operatorname {ratio}( {\mathrm{cod}}(G))$
is
$\operatorname {ratio}( {\mathrm{cod}}(G))$
is
![]() $q- 1$
, where
$q- 1$
, where
![]() $q \geq 27$
.
$q \geq 27$
.
Suppose
![]() $G/N \cong {\mathrm{PSU}}(3,s)$
with
$G/N \cong {\mathrm{PSU}}(3,s)$
with
![]() $4 < s \equiv -1\ (\bmod \ 3)$
. Note that
$4 < s \equiv -1\ (\bmod \ 3)$
. Note that
![]() $s-1, s+1 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
, and the only nontrivial integers in
$s-1, s+1 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
, and the only nontrivial integers in
![]() $\operatorname {ratio}( {\mathrm{cod}}(G))$
are
$\operatorname {ratio}( {\mathrm{cod}}(G))$
are
![]() $q-1$
, q,
$q-1$
, q,
![]() $q+1$
, where q is a power of
$q+1$
, where q is a power of
![]() $3$
and
$3$
and
![]() $q \geq 27$
. This will force
$q \geq 27$
. This will force
![]() $s=q$
, which is a contradiction since
$s=q$
, which is a contradiction since
![]() $q^3(q+1)^2 \not \in {\mathrm{cod}}(G)$
.
$q^3(q+1)^2 \not \in {\mathrm{cod}}(G)$
.
Suppose
![]() $| {\mathrm{cod}}(G/N)| = 10$
. Then
$| {\mathrm{cod}}(G/N)| = 10$
. Then
![]() $G/N \cong M_{22}$
. Note that
$G/N \cong M_{22}$
. Note that
![]() $11 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the only nontrivial integer in
$11 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the only nontrivial integer in
![]() $\operatorname {ratio}( {\mathrm{cod}}(G))$
is q, where
$\operatorname {ratio}( {\mathrm{cod}}(G))$
is q, where
![]() $q \geq 27$
.
$q \geq 27$
.
Suppose
![]() $| {\mathrm{cod}}(G/N)| = 11$
. Then
$| {\mathrm{cod}}(G/N)| = 11$
. Then
![]() $G/N \cong { {\mathrm{PSL}}}(4,2), M_{12}, M_{23}$
or
$G/N \cong { {\mathrm{PSL}}}(4,2), M_{12}, M_{23}$
or
![]() ${}^2G_2(3^{2s+1})$
, where
${}^2G_2(3^{2s+1})$
, where
![]() $s\geq 1$
.
$s\geq 1$
.
Suppose
![]() $G/N \cong {\mathrm{PSL}}(4, 2)$
. Note that
$G/N \cong {\mathrm{PSL}}(4, 2)$
. Note that
![]() $2 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
$2 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
![]() $\operatorname {ratio}( {\mathrm{cod}}(G))$
is
$\operatorname {ratio}( {\mathrm{cod}}(G))$
is
![]() $q- 1$
, where
$q- 1$
, where
![]() $q \geq 27$
.
$q \geq 27$
.
Suppose
![]() $G/N \cong M_{12}$
. Note that
$G/N \cong M_{12}$
. Note that
![]() $5 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
$5 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
![]() $\operatorname {ratio}( {\mathrm{cod}}(G))$
is
$\operatorname {ratio}( {\mathrm{cod}}(G))$
is
![]() $q- 1$
, where
$q- 1$
, where
![]() $q \geq 27$
.
$q \geq 27$
.
Suppose
![]() $G/N \cong M_{23}$
. Note that
$G/N \cong M_{23}$
. Note that
![]() $8 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
$8 \in \operatorname {ratio}( {\mathrm{cod}}(G/N))$
. This is a contradiction since the smallest nontrivial integer in
![]() $\operatorname {ratio}( {\mathrm{cod}}(G))$
is
$\operatorname {ratio}( {\mathrm{cod}}(G))$
is
![]() $q- 1$
, where
$q- 1$
, where
![]() $q \geq 27$
.
$q \geq 27$
.
Suppose
![]() $G/N \cong {}^2G_2(3^{2s+1})$
,
$G/N \cong {}^2G_2(3^{2s+1})$
,
![]() $s\ge 1$
. Comparing the smallest nontrival odd codegree of each set, we see that
$s\ge 1$
. Comparing the smallest nontrival odd codegree of each set, we see that
![]() $q=3^{2s+1}$
. Thus,
$q=3^{2s+1}$
. Thus,
![]() $G/N \cong {}^2G_2(3^{2f+1})$
.
$G/N \cong {}^2G_2(3^{2f+1})$
.
We now prove the main result of this paper.
Theorem 3.2. Let G be a group such that
![]() $ {\mathrm{cod}}(G)= {\mathrm{cod}}({}^2G_2(q))$
, where
$ {\mathrm{cod}}(G)= {\mathrm{cod}}({}^2G_2(q))$
, where
![]() $q=3^{2f+1}$
,
$q=3^{2f+1}$
,
![]() $f \geq 1$
. Then
$f \geq 1$
. Then
![]() $G \cong {}^2G_2(q)$
.
$G \cong {}^2G_2(q)$
.
Proof. Let G be a group with
![]() $ {\mathrm{cod}}(G) = {\mathrm{cod}}({}^2G_2(q))$
. Let N be a maximal normal subgroup of G. Then,
$ {\mathrm{cod}}(G) = {\mathrm{cod}}({}^2G_2(q))$
. Let N be a maximal normal subgroup of G. Then,
![]() $G/N \cong {}^2G_2(q)$
by Lemma 3.1. Assume to the contrary that G is a minimal counterexample. By the choice of G, N is a minimal normal subgroup of G. Otherwise there exists a nontrivial normal subgroup L of G such that L is included in N. Then
$G/N \cong {}^2G_2(q)$
by Lemma 3.1. Assume to the contrary that G is a minimal counterexample. By the choice of G, N is a minimal normal subgroup of G. Otherwise there exists a nontrivial normal subgroup L of G such that L is included in N. Then
![]() $ {\mathrm{cod}}(G/L)= {\mathrm{cod}}(G)$
for
$ {\mathrm{cod}}(G/L)= {\mathrm{cod}}(G)$
for
![]() $ {\mathrm{cod}}(G)= {\mathrm{cod}}(G/N)\subseteq {\mathrm{cod}}(G/L) \subseteq {\mathrm{cod}}(G)$
and
$ {\mathrm{cod}}(G)= {\mathrm{cod}}(G/N)\subseteq {\mathrm{cod}}(G/L) \subseteq {\mathrm{cod}}(G)$
and
![]() $G/L\cong {}^2G_2(q)$
because G is a minimal counterexample, which is a contradiction.
$G/L\cong {}^2G_2(q)$
because G is a minimal counterexample, which is a contradiction.
Step 1: N is the unique minimal normal subgroup of G. Otherwise, assume M is another minimal normal subgroup of G. Then
![]() $G=N\times M$
because
$G=N\times M$
because
![]() $G/N$
is simple and
$G/N$
is simple and
![]() $N\cong M\cong {}^2G_2(q)$
because M is also a maximal normal subgroup of G. Choose
$N\cong M\cong {}^2G_2(q)$
because M is also a maximal normal subgroup of G. Choose
![]() $\psi _1\in \mbox {Irr}(N)$
and
$\psi _1\in \mbox {Irr}(N)$
and
![]() $\psi _2\in \mbox {Irr}(M)$
such that
$\psi _2\in \mbox {Irr}(M)$
such that
![]() $ {\mathrm{cod}}(\psi _1)= {\mathrm{cod}}(\psi _2)=\max ( {\mathrm{cod}}({}^2G_2(q)))$
. Set
$ {\mathrm{cod}}(\psi _1)= {\mathrm{cod}}(\psi _2)=\max ( {\mathrm{cod}}({}^2G_2(q)))$
. Set
![]() $\chi =\psi _1 \cdot \psi _2\in \mbox {Irr}(G)$
. Then
$\chi =\psi _1 \cdot \psi _2\in \mbox {Irr}(G)$
. Then
![]() $ {\mathrm{cod}}(\,\chi )=(\max ( {\mathrm{cod}}({}^2G_2(q))))^2\notin {\mathrm{cod}}(G)$
, which is a contradiction.
$ {\mathrm{cod}}(\,\chi )=(\max ( {\mathrm{cod}}({}^2G_2(q))))^2\notin {\mathrm{cod}}(G)$
, which is a contradiction.
Set
![]() $\mbox {Irr}(G|N)=\{\,\chi \in \mbox {Irr}(G)|\,N$
is not contained in the kernel of
$\mbox {Irr}(G|N)=\{\,\chi \in \mbox {Irr}(G)|\,N$
is not contained in the kernel of
![]() $\chi \}$
.
$\chi \}$
.
Step 2:
![]() $\chi $
is faithful for each
$\chi $
is faithful for each
![]() $\chi \in \mbox {Irr}(G|N)$
. Since N is not contained in the kernel of
$\chi \in \mbox {Irr}(G|N)$
. Since N is not contained in the kernel of
![]() $\chi $
for each
$\chi $
for each
![]() $\chi \in \mbox {Irr}(G|N)$
, the kernel of
$\chi \in \mbox {Irr}(G|N)$
, the kernel of
![]() $\chi $
is trivial by Step 1.
$\chi $
is trivial by Step 1.
Step 3: N is elementary abelian. Assume to the contrary that N is not abelian. Then
![]() $N=S^n$
, where S is a nonabelian simple group and
$N=S^n$
, where S is a nonabelian simple group and
![]() $n\in \mathbb {N}$
. By Theorems 2, 3 and 4 and Lemma 5 in [Reference Bianchi, Chillag, Lewis and Pacifici5], we see that there exists a nonprincipal character
$n\in \mathbb {N}$
. By Theorems 2, 3 and 4 and Lemma 5 in [Reference Bianchi, Chillag, Lewis and Pacifici5], we see that there exists a nonprincipal character
![]() $\psi \in \mbox {Irr}(N)$
that extends to some
$\psi \in \mbox {Irr}(N)$
that extends to some
![]() $\chi \in \mbox {Irr}(G)$
. Then
$\chi \in \mbox {Irr}(G)$
. Then
![]() $\ker (\,\chi )=1$
by Step 2 and
$\ker (\,\chi )=1$
by Step 2 and
![]() $ {\mathrm{cod}}(\,\chi )=|G|/\chi (1)=|G/N|\cdot |N|/\psi (1)$
. This is a contradiction since
$ {\mathrm{cod}}(\,\chi )=|G|/\chi (1)=|G/N|\cdot |N|/\psi (1)$
. This is a contradiction since
![]() $|G/N|$
is divisible by
$|G/N|$
is divisible by
![]() $ {\mathrm{cod}}(\,\chi )$
.
$ {\mathrm{cod}}(\,\chi )$
.
Step 4: It is enough to assume that
![]() $\mathbf {C}_G(N)=N$
. We note that
$\mathbf {C}_G(N)=N$
. We note that
![]() ${\textbf {{C}}}_G(N) \unlhd G$
. As N is abelian by Step 3, either
${\textbf {{C}}}_G(N) \unlhd G$
. As N is abelian by Step 3, either
![]() ${\textbf {{C}}}_G(N) = G$
or
${\textbf {{C}}}_G(N) = G$
or
![]() ${\textbf {{C}}}_G(N) =~N$
.
${\textbf {{C}}}_G(N) =~N$
.
We now prove the result in the case
![]() ${\textbf {{C}}}_G(N) = G$
. Assume so. Then N is contained in the centre
${\textbf {{C}}}_G(N) = G$
. Assume so. Then N is contained in the centre
![]() ${\textbf {Z}}(G)$
of G. Since G is perfect,
${\textbf {Z}}(G)$
of G. Since G is perfect,
![]() ${\textbf {Z}}(G)=N$
and N is isomorphic to a subgroup of the Schur multiplier of
${\textbf {Z}}(G)=N$
and N is isomorphic to a subgroup of the Schur multiplier of
![]() $G/N$
[Reference Isaacs10, Corollary 11.20]. This forces N to be trivial as
$G/N$
[Reference Isaacs10, Corollary 11.20]. This forces N to be trivial as
![]() ${}^2G_2(q)$
has trivial Schur multiplier, and we are done.
${}^2G_2(q)$
has trivial Schur multiplier, and we are done.
Step 5: Let
![]() $\lambda $
be a nonprincipal character in
$\lambda $
be a nonprincipal character in
![]() $\mbox {Irr}(N)$
and
$\mbox {Irr}(N)$
and
![]() $\theta \in \mbox {Irr}(I_G(\lambda )|\lambda )$
. We show that
$\theta \in \mbox {Irr}(I_G(\lambda )|\lambda )$
. We show that
![]() ${|I_G(\lambda )|}/{\theta (1)} \in {\mathrm{cod}}(G)$
. Also,
${|I_G(\lambda )|}/{\theta (1)} \in {\mathrm{cod}}(G)$
. Also,
![]() $\theta (1)$
divides
$\theta (1)$
divides
![]() $|I_G(\lambda )/N|$
and
$|I_G(\lambda )/N|$
and
![]() $|N|$
divides
$|N|$
divides
![]() $|G/N|$
. Let
$|G/N|$
. Let
![]() $\lambda $
be a nonprincipal character in
$\lambda $
be a nonprincipal character in
![]() $\mbox {Irr}(N)$
. Given
$\mbox {Irr}(N)$
. Given
![]() $\theta \in \mbox {Irr}(I_G(\lambda )|\lambda )$
. Note that
$\theta \in \mbox {Irr}(I_G(\lambda )|\lambda )$
. Note that
![]() $\chi =\theta ^G\in \mbox {Irr}(G)$
and
$\chi =\theta ^G\in \mbox {Irr}(G)$
and
![]() $\chi (1)=|G:I_G(\lambda )|\cdot \theta (1)$
by Clifford theory (see [Reference Isaacs10, Ch. 6]). Then
$\chi (1)=|G:I_G(\lambda )|\cdot \theta (1)$
by Clifford theory (see [Reference Isaacs10, Ch. 6]). Then
![]() $\ker (\,\chi )=1$
by Step 2 and
$\ker (\,\chi )=1$
by Step 2 and
![]() $ {\mathrm{cod}}(\,\chi )={|I_G(\lambda )|}/{\theta (1)}$
. In particular,
$ {\mathrm{cod}}(\,\chi )={|I_G(\lambda )|}/{\theta (1)}$
. In particular,
![]() $\theta (1)$
divides
$\theta (1)$
divides
![]() $|I_G(\lambda )/N|$
, and then
$|I_G(\lambda )/N|$
, and then
![]() $|N|$
divides
$|N|$
divides
![]() ${|I_G(\lambda )|}/{\theta (1)}$
. Since
${|I_G(\lambda )|}/{\theta (1)}$
. Since
![]() $ {\mathrm{cod}}(G)= {\mathrm{cod}}(G/N)$
and
$ {\mathrm{cod}}(G)= {\mathrm{cod}}(G/N)$
and
![]() $|G/N|$
is divisible by every element in
$|G/N|$
is divisible by every element in
![]() $ {\mathrm{cod}}(G/N)$
, we have
$ {\mathrm{cod}}(G/N)$
, we have
![]() $|N|\mid |G/N|$
.
$|N|\mid |G/N|$
.
Step 6: Final contradiction. By Step 3, N is an elementary abelian r-subgroup for some prime r and we assume
![]() $|N|=r^n$
,
$|N|=r^n$
,
![]() $n\in \mathbb {N}$
. By the normaliser–centraliser theorem,
$n\in \mathbb {N}$
. By the normaliser–centraliser theorem,
![]() $n> 1$
.
$n> 1$
.
Let
![]() $\lambda \in \mbox {Irr}(N)$
be a nonprincipal character and
$\lambda \in \mbox {Irr}(N)$
be a nonprincipal character and
![]() $T:=I_G(\lambda )$
. By Step 5,
$T:=I_G(\lambda )$
. By Step 5,
![]() ${|T|}/{\theta (1)}\in {\mathrm{cod}}(G)$
for all
${|T|}/{\theta (1)}\in {\mathrm{cod}}(G)$
for all
![]() $\theta \in \mbox {Irr}(T|\lambda )$
.
$\theta \in \mbox {Irr}(T|\lambda )$
.
Since N is abelian by Step 1,
![]() $|\mbox {Irr}(N)|=|N|$
. Therefore,
$|\mbox {Irr}(N)|=|N|$
. Therefore,
![]() $|N|=|\mbox {Irr}(N)|> |G:T|$
since
$|N|=|\mbox {Irr}(N)|> |G:T|$
since
![]() $|G:T|$
is the number of conjugates of
$|G:T|$
is the number of conjugates of
![]() $\lambda $
in G which are all contained in
$\lambda $
in G which are all contained in
![]() $\mbox {Irr}(N)$
.
$\mbox {Irr}(N)$
.
We now show that
![]() $q^3$
is the largest power of a prime that divides the order of
$q^3$
is the largest power of a prime that divides the order of
![]() ${}^2G_2(q)$
. Note that the order of
${}^2G_2(q)$
. Note that the order of
![]() ${}^2G_2(q)$
is
${}^2G_2(q)$
is
![]() $q^3(q^3+1)(q-1)$
. We first observe that
$q^3(q^3+1)(q-1)$
. We first observe that
![]() $q^3+1=2^k$
has no integer solution, and thus
$q^3+1=2^k$
has no integer solution, and thus
![]() $q^3+1$
is divisible by a prime greater than or equal to
$q^3+1$
is divisible by a prime greater than or equal to
![]() $5$
. We also note that either
$5$
. We also note that either
![]() $q^3+1$
or
$q^3+1$
or
![]() $q-1$
is divisible by
$q-1$
is divisible by
![]() $4$
but not both, and thus the largest power of
$4$
but not both, and thus the largest power of
![]() $2$
that divides
$2$
that divides
![]() $(q^3+1)(q-1)$
is less than
$(q^3+1)(q-1)$
is less than
![]() $q^3$
. Suppose that r is an odd prime that divides
$q^3$
. Suppose that r is an odd prime that divides
![]() $(q^3+1)(q-1)$
. Since
$(q^3+1)(q-1)$
. Since
![]() $\gcd (q+1,q-1)=2$
, the largest power of r that divides
$\gcd (q+1,q-1)=2$
, the largest power of r that divides
![]() $(q^3+1)(q-1)$
is also less than
$(q^3+1)(q-1)$
is also less than
![]() $q^3$
. Thus,
$q^3$
. Thus,
![]() $q^3$
is the largest power of a prime that divides the order of
$q^3$
is the largest power of a prime that divides the order of
![]() ${}^2G_2(q)$
. Thus,
${}^2G_2(q)$
. Thus,
![]() $|N| \leq q^3$
.
$|N| \leq q^3$
.
Let K be a maximal subgroup of
![]() ${}^2G_2(q)$
such that
${}^2G_2(q)$
such that
![]() $T/N \leq K$
. If K is of type P in Lemma 2.3, then
$T/N \leq K$
. If K is of type P in Lemma 2.3, then
![]() $|G:T| \ge q^3+1$
, and it is clear that
$|G:T| \ge q^3+1$
, and it is clear that
![]() $q^3+1>q^3$
, which is a contradiction. If K is of type
$q^3+1>q^3$
, which is a contradiction. If K is of type
![]() $ C_{R_{0}(i)}$
, then
$ C_{R_{0}(i)}$
, then
![]() $|G:T| \ge q^2 (q^2 - q + 1)> q^3 $
, which is a contradiction. If K is of type
$|G:T| \ge q^2 (q^2 - q + 1)> q^3 $
, which is a contradiction. If K is of type
![]() $N_{R_{0} \langle i ,j \rangle }$
, then
$N_{R_{0} \langle i ,j \rangle }$
, then
![]() $|G:T| \ge { q^3( q^2 - q + 1 ) ( q - 1) }/{ 12 (q+1) }$
, thus
$|G:T| \ge { q^3( q^2 - q + 1 ) ( q - 1) }/{ 12 (q+1) }$
, thus
![]() $|G:T|> q^3$
, which is a contradiction. If K is of type
$|G:T|> q^3$
, which is a contradiction. If K is of type
![]() $M^{+}W^{+}$
, then
$M^{+}W^{+}$
, then
![]() $|G:T| \ge { q^3( q^2 - q + 1 ) ( q - 1) }/{ 6 ( q +\! \sqrt { 3q } + 1 )}$
, and thus
$|G:T| \ge { q^3( q^2 - q + 1 ) ( q - 1) }/{ 6 ( q +\! \sqrt { 3q } + 1 )}$
, and thus
![]() $|G:T|> q^3$
, which is a contradiction. If K is of type
$|G:T|> q^3$
, which is a contradiction. If K is of type
![]() $M^{-}W^{-}$
, then
$M^{-}W^{-}$
, then
![]() $|G:T| \ge { q^3( q^2 - q + 1 ) ( q - 1) }/{ 6 ( q -\! \sqrt { 3q } + 1 )}$
, and thus
$|G:T| \ge { q^3( q^2 - q + 1 ) ( q - 1) }/{ 6 ( q -\! \sqrt { 3q } + 1 )}$
, and thus
![]() $|G:T|> q^3$
, which is a contradiction. If K is of type
$|G:T|> q^3$
, which is a contradiction. If K is of type
![]() $C_{R_0}(\Psi _{ \alpha })$
, then
$C_{R_0}(\Psi _{ \alpha })$
, then
![]() $|G:T| \ge {q^3(q^3+1)(q-1)}/{q_0^3(q_0^3+1)(q_0-1)}$
, where
$|G:T| \ge {q^3(q^3+1)(q-1)}/{q_0^3(q_0^3+1)(q_0-1)}$
, where
![]() $q=q_0^{\alpha }$
,
$q=q_0^{\alpha }$
,
![]() $\alpha $
a prime. Thus,
$\alpha $
a prime. Thus,
![]() $|G:T|> q^ {3}$
, which is a contradiction.
$|G:T|> q^ {3}$
, which is a contradiction.
Acknowledgement
The authors are grateful to the referee for the valuable suggestions which improved the manuscript.