Hostname: page-component-77c89778f8-swr86 Total loading time: 0 Render date: 2024-07-16T11:38:58.537Z Has data issue: false hasContentIssue false
  • English
  • Français

Property preserving operators

Published online by Cambridge University Press:  17 April 2009

Evelyn M. Silvia
Evelyn M. Silvia
Affiliation:
Department of Mathematics, University of California, Davis, Davis, CA 95616United States of America.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S denote the class of functions of the form 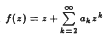that are analytic and univalent in |z| < 1. Given f ∈ S and a, b, c, real numbers other than 0, −1, −2,…, let Ω(a, b, C; f) = F(a, b, C; z)* f(z) where 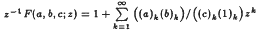is a hypergeometric Gauss function with (a)0 = 1 and (a)k = a(a + 1) … (a + k − 1) and * denotes the Hadamard product. For qn(z) = z + a2z2 + … + anzn (an ≠ 0, n = 5,6) in S, it is shown that 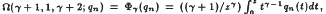, is univalent in |z| < 1. This extends the result previously known for n = 3 and n = 4. Also, we obtain a necessary and sufficient condition involving a, b, and c such that Ω(a, b, c;·) preserves the subclass of S consisting of starlike functions of order α, 0 ≤ α ≤ 1, with ak 0.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 39 , Issue 3 , June 1989 , pp. 397 - 404
Copyright
Copyright © Australian Mathematical Society 1989

References

[1] Biernacki, M., ‘Sur l'integral des fonctions univalentes’, Bull. Acad. Polon. Sci., Ser. Math. Astron. Phys. 8 (1980), 29–34.Google Scholar
[2] Frank, J.L., ‘Subordination and convex univalent polynomials’, J. Reine Angew. Math. 290 (1977), 63–69.Google Scholar
[3] Khokhlov, Y.E., ‘Convolutory operators preserving univalent functions’, Ukrainian Math. J. 37 (1985), 220–226.Google Scholar
[4] Krzyz, J., ‘The radius of close-to-convexity within the family of univalent functions’, Bull. Acad. Polon. Sci., Ser. Math. Astron. Phys. 10 (1962), 201–204.Google Scholar
[5] Krzyz, J. and Lewandowski, Z., ‘On the integral of univalent functions’, Bull. Acad. Polon. Sci., Ser. Math. Astron. Phys. 11 (1963), 447–448.Google Scholar
[6] Krzyz, J. and Rahman, I., ‘Univalent polynomials of small degree’, Ann. Univ. Mariae Curie-Sklodowska Sect. A 21 (1967), 79–90.Google Scholar
[7] Marden, M., Geometry of Polynomials, Amer. Math. Soc. Surveys, No. 3, 1963.Google Scholar
[8] Ruscheweyh, St., ‘New criteria for univalent functions’, Proc. Amer. Math. Soc. 49 (1975), 109–115.CrossRefGoogle Scholar
[9] Ruscheweyh, St. and Sheil-Small, T., ‘Hadamard products of schlicht functions and the Polya-Schoenberg conjecture’, Comment. Math. Helv. 48 (1973), 119–135.CrossRefGoogle Scholar
[10] Silverman, H., ‘Univalent functions with negative coefficients’, Proc. Amer. Math. Soc 51 (1975), 109–116.CrossRefGoogle Scholar
[11] Silverman, H. and Silvia, E., ‘Univalence preserving operators’, Complex Variables Theory Appl. 5 (1986), 313–321.Google Scholar
[12] Silverman, H. and Ziegler, M., ‘Functions of positive real part with negative coefficients’, Houston J. Math. (2) 4 (1978), 269–275.Google Scholar
[13] Suffridge, T.J., ‘On univalent polynomials’, J. London Math. Soc. 44 (1969), 496–504.Google Scholar
[14] Wittaker, E.T. and Watson, G.N., A Course of Modern Analysis, 4th edition reprinted (Cambridge University Press, Cambridge, 1980).Google Scholar