Article contents
ON ADDITIVE REPRESENTATION FUNCTIONS
Published online by Cambridge University Press: 02 May 2017
Abstract
For any finite abelian group 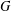 $G$ with
$G$ with 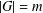 $|G|=m$,
$|G|=m$, 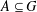 $A\subseteq G$ and
$A\subseteq G$ and 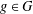 $g\in G$, let
$g\in G$, let 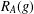 $R_{A}(g)$ be the number of solutions of the equation
$R_{A}(g)$ be the number of solutions of the equation 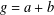 $g=a+b$,
$g=a+b$, 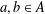 $a,b\in A$. Recently, Sándor and Yang [‘A lower bound of Ruzsa’s number related to the Erdős–Turán conjecture’, Preprint, 2016, arXiv:1612.08722v1] proved that, if
$a,b\in A$. Recently, Sándor and Yang [‘A lower bound of Ruzsa’s number related to the Erdős–Turán conjecture’, Preprint, 2016, arXiv:1612.08722v1] proved that, if 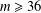 $m\geq 36$ and
$m\geq 36$ and 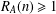 $R_{A}(n)\geq 1$ for all
$R_{A}(n)\geq 1$ for all 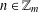 $n\in \mathbb{Z}_{m}$, then there exists
$n\in \mathbb{Z}_{m}$, then there exists 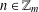 $n\in \mathbb{Z}_{m}$ such that
$n\in \mathbb{Z}_{m}$ such that 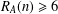 $R_{A}(n)\geq 6$. In this paper, for any finite abelian group
$R_{A}(n)\geq 6$. In this paper, for any finite abelian group 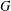 $G$ with
$G$ with 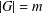 $|G|=m$ and
$|G|=m$ and 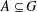 $A\subseteq G$, we prove that (a) if the number of
$A\subseteq G$, we prove that (a) if the number of 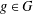 $g\in G$ with
$g\in G$ with 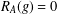 $R_{A}(g)=0$ does not exceed
$R_{A}(g)=0$ does not exceed 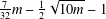 $\frac{7}{32}m-\frac{1}{2}\sqrt{10m}-1$, then there exists
$\frac{7}{32}m-\frac{1}{2}\sqrt{10m}-1$, then there exists 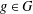 $g\in G$ such that
$g\in G$ such that 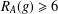 $R_{A}(g)\geq 6$; (b) if
$R_{A}(g)\geq 6$; (b) if 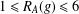 $1\leq R_{A}(g)\leq 6$ for all
$1\leq R_{A}(g)\leq 6$ for all 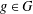 $g\in G$, then the number of
$g\in G$, then the number of 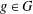 $g\in G$ with
$g\in G$ with 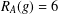 $R_{A}(g)=6$ is more than
$R_{A}(g)=6$ is more than 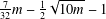 $\frac{7}{32}m-\frac{1}{2}\sqrt{10m}-1$.
$\frac{7}{32}m-\frac{1}{2}\sqrt{10m}-1$.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 380 - 388
- Copyright
- © 2017 Australian Mathematical Publishing Association Inc.
Footnotes
This work was supported by the National Natural Science Foundation of China, Grant No. 11371195, and a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.
References
- 1
- Cited by




