Article contents
MULTIDIMENSIONAL HARDY-TYPE INEQUALITIES VIA CONVEXITY
Published online by Cambridge University Press: 01 April 2008
Abstract
Let an almost everywhere positive function Φ be convex for p>1 and p<0, concave for p∈(0,1), and such that Axp≤Φ(x)≤Bxp holds on 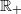 for some positive constants A≤B. In this paper we derive a class of general integral multidimensional Hardy-type inequalities with power weights, whose left-hand sides involve
for some positive constants A≤B. In this paper we derive a class of general integral multidimensional Hardy-type inequalities with power weights, whose left-hand sides involve 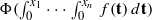 instead of
instead of 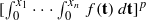 , while the corresponding right-hand sides remain as in the classical Hardy’s inequality and have explicit constants in front of integrals. We also prove the related dual inequalities. The relations obtained are new even for the one-dimensional case and they unify and extend several inequalities of Hardy type known in the literature.
, while the corresponding right-hand sides remain as in the classical Hardy’s inequality and have explicit constants in front of integrals. We also prove the related dual inequalities. The relations obtained are new even for the one-dimensional case and they unify and extend several inequalities of Hardy type known in the literature.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © 2008 Australian Mathematical Society
Footnotes
The research of the first author was supported by the Swedish Institute under the Guest Fellowship Programme 210/05529/2005. The research of the third author was supported by the Croatian Ministry of Science, Education and Sports, under Research Grant 058-1170889-1050.
References
- 5
- Cited by




