Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-23T05:50:31.549Z Has data issue: false hasContentIssue false
  • English
  • Français

MAPPINGS OF CONSERVATIVE DISTANCES IN 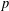$p$-NORMED SPACES (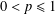$0<p\leq 1$)

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  02 November 2016

XUJIAN HUANG  and
DONGNI TAN
XUJIAN HUANG
Affiliation:
Department of Mathematics, Tianjin University of Technology, 300384 Tianjin, China email huangxujian86@sina.cn
DONGNI TAN*
Affiliation:
Department of Mathematics, Tianjin University of Technology, 300384 Tianjin, China email tandongni0608@sina.cn
*
✉tandongni0608@sina.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that any mapping between two real 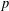$p$-normed spaces, which preserves the unit distance and the midpoint of segments with distance 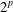$2^{p}$, is an isometry. Making use of it, we provide an alternative proof of some known results on the Aleksandrov question in normed spaces and also generalise these known results to 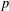$p$-normed spaces.

Keywords

Aleksandrov problemp-strictly convexisometryp-normed space

MSC classification

Primary: 46B04: Isometric theory of Banach spaces
Secondary: 46B20: Geometry and structure of normed linear spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 2 , April 2017 , pp. 291 - 298
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

The authors are supported by the Natural Science Foundation of China (grant nos. 11201337, 11201338, 11371201 and 11301384).

References

Aleksandrov, A. D., ‘Mappings of families of sets’, Soviet Math. Dokl. 11 (1970), 116–120.Google Scholar
Baker, J. A., ‘Isometries in normed spaces’, Amer. Math. Monthly 78 (1971), 655–658.Google Scholar
Beckman, F. S. and Quarles, D. A., ‘On isometries of Euclidean spaces’, Proc. Amer. Math. Soc. 4 (1953), 810–815.Google Scholar
Benz, W., ‘Isometrien in normierten Räumen’, Aequationes Math. 29 (1985), 204–209.Google Scholar
Benz, W. and Berens, H., ‘A contribution to a theorem of Ulam and Mazur’, Aequationes Math. 34 (1987), 61–63.Google Scholar
Fleming, R. J. and Jameson, J. E., Isometries on Banach Spaces: Function Spaces (Chapman and Hall/CRC, Boca Raton, FL, 2003).Google Scholar
Gehér, G. P., ‘A contribution to the Aleksandrov conservative distance problem in two dimensions’, Linear Algebra Appl. 481 (2015), 280–287.Google Scholar
Juhász, R., ‘Another proof of the Beckman–Quarles theorem’, Adv. Geom. 15(4) (2015), 519–521.Google Scholar
Köthe, G., Topological Vector Spaces I (Springer, Berlin, 1969).Google Scholar
Ling, J. M., ‘A normed space with the Beckman–Quarles property’, Contrib. Algebra Geom. 48(1) (2007), 131–139.Google Scholar
Ma, Y., ‘The Aleksandrov problem for unit distance preserving mapping’, Acta Math. Sci. 20 (2000), 359–364.Google Scholar
Mazur, S. and Ulam, S., ‘Sur les transformations isométriques d’espaces vectoriels normés’, C. R. Math. Acad. Sci. Paris 194 (1932), 946–948.Google Scholar
Rassias, Th. M. and Šemrl, P., ‘On the Mazur–Ulam problem and the Aleksandrov problem for unit distance preserving mappings’, Proc. Amer. Math. Soc. 118 (1993), 919–925.CrossRefGoogle Scholar
Valentine, J. E., ‘Some implications of Euclid’s Proposition 7’, Math. Japon. 28 (1983), 421–425.Google Scholar