Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-16T14:49:10.916Z Has data issue: false hasContentIssue false
  • English
  • Français

Jackson's Theorem for finite products and homomorphic images of locally compact abelian groups

Published online by Cambridge University Press:  17 April 2009

Walter R. Bloom
Walter R. Bloom
Affiliation:
Department of Mathematics, University of Tasmania, Hobart, Tasmania;
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a Hausdorff locally compact abelian group. The author has shown (Bull. Austral. Math. Soc. 10 (1974), 59–66) that, given ε > 0 and a certain base {Vi}i∈I of symmetric open neighbourhoods of zero, the algebra L1(G) admits a bounded positive approximate unit {ki}i∈I such that for every p–th integrable function f on G,

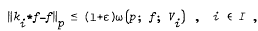
where ω(p; f; Vi) denotes the mean modulus of continuity with exponent p of f. The purpose of this paper is to obtain {ki}i∈I (as above) with a simple dependence of supp 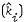on {ki}i∈I on Vi; this is achieved for finite products and homomorphic images of groups for which such a simple dependence is known. The results obtained are used to give a simplified proof of the classical Jackson's Theorem for the circle group, and an analogue of this theorem for the a-adic solenoid.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 12 , Issue 2 , April 1975 , pp. 301 - 309
Copyright
Copyright © Australian Mathematical Society 1975

References

[1]Bloom, Walter R., “Jackson's Theorem for locally compact abelian groups”, Bull. Austral. Math. Soc. 10 (1974), 59–66.CrossRefGoogle Scholar
[2]Hewitt, Edwin and Ross, Kenneth A., Abstract harmonic analysis, Volume I (Die Grundlehren der mathematischen Wissenschaften, 115. Academic Press, New York; Springer-Verlag, Berlin, Göttingen, Heidelberg, 1963).Google Scholar
[3]Hewitt, Edwin and Ross, Kenneth A., Abstract harmonic analysis, Volume II (Die Grundlehren der mathematischen Wissenschaften, 152. Springer-Verlag, Berlin, Heidelberg, New York, 1970).Google Scholar
[4]Korovkin, P.P., Linear operators and approximation theory (translated from the Russian ed. (1959). Hindustan Publishing Corp. (India), Delhi, 1960).Google Scholar
[5]Reiter, Hans, Classical harmonia analysis and locally compact groups (Clarendon Press, Oxford, 1968).Google Scholar