Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-20T01:51:31.613Z Has data issue: false hasContentIssue false
  • English
  • Français

A GENERAL POSITION PROBLEM IN GRAPH THEORY

Part of: Theory of computing Graph theory

Published online by Cambridge University Press:  18 July 2018

PAUL MANUEL Open the ORCID record for PAUL MANUEL [Opens in a new window]  and
SANDI KLAVŽAR
PAUL MANUEL*
Affiliation:
Department of Information Science, College of Computing Science and Engineering, Kuwait University, Kuwait email pauldmanuel@gmail.com
SANDI KLAVŽAR
Affiliation:
Faculty of Mathematics and Physics, University of Ljubljana, Slovenia Faculty of Natural Sciences and Mathematics, University of Maribor, Slovenia Institute of Mathematics, Physics and Mechanics, Ljubljana, Slovenia email sandi.klavzar@fmf.uni-lj.si
*
✉pauldmanuel@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

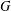The paper introduces a graph theory variation of the general position problem: given a graph $G$, determine a largest set 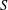$S$ of vertices of 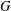$G$ such that no three vertices of 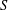$S$ lie on a common geodesic. Such a set is a max-gp-set of 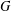$G$ and its size is the gp-number 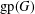$\text{gp}(G)$ of 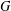$G$. Upper bounds on 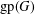$\text{gp}(G)$ in terms of different isometric covers are given and used to determine the gp-number of several classes of graphs. Connections between general position sets and packings are investigated and used to give lower bounds on the gp-number. It is also proved that the general position problem is NP-complete.

Keywords

general position problemisometric subgraphpackingindependence numbercomputational complexity

MSC classification

Primary: 05C12: Distance in graphs
Secondary: 05C70: Factorization, matching, partitioning, covering and packing 68Q25: Analysis of algorithms and problem complexity
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 2 , October 2018 , pp. 177 - 187
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported and funded by Kuwait University, Research Project No. QI 02/17.

References

Barnaby, M., Raimondi, F., Chen, T. and Martin, J., ‘The packing chromatic number of the infinite square lattice is between 13 and 15’, Discrete Appl. Math. 225 (2017), 136–142.Google Scholar
Beaudou, L., Gravier, S. and Meslem, K., ‘Subdivided graphs as isometric subgraphs of Hamming graphs’, European J. Combin. 30 (2009), 1062–1070.Google Scholar
Brešar, B., Klavžar, S., Rall, D. F. and Wash, K., ‘Packing chromatic number, (1, 1, 2, 2)-colorings, and characterizing the Petersen graph’, Aequationes Math. 91 (2017), 169–184.Google Scholar
Dankelmann, P., ‘Average distance and generalised packing in graphs’, Discrete Math. 310 (2010), 2334–2344.Google Scholar
Dudeney, H. E., Amusements in Mathematics (Nelson, Edinburgh, 1917).Google Scholar
Fitzpatrick, S. L., ‘The isometric path number of the Cartesian product of paths’, Congr. Numer. 137 (1999), 109–119.Google Scholar
Froese, V., Kanj, I., Nichterlein, A. and Niedermeier, R., ‘Finding points in general position’, Internat. J. Comput. Geom. Appl. 27 (2017), 277–296.Google Scholar
Garey, M. R. and Johnson, D. S., Computers and Intractability: A Guide to the Theory of NP-Completeness (W. H. Freeman, New York, 1979).Google Scholar
Goddard, W. and Xu, H., ‘The S-packing chromatic number of a graph’, Discuss. Math. Graph Theory 32 (2012), 795–806.Google Scholar
Hartnell, B. and Whitehead, C. A., ‘On k-packings of graphs’, Ars Combin. 47 (1997), 97–108.Google Scholar
Meir, A. and Moon, J. W., ‘Relations between packing and covering numbers of a tree’, Pacific J. Math. 61 (1975), 225–233.Google Scholar
Misiak, A., Stpień, Z., Szymaszkiewicz, A., Szymaszkiewicz, L. and Zwierzchowski, M., ‘A note on the no-three-in-line problem on a torus’, Discrete Math. 339 (2016), 217–221.Google Scholar
Pan, J.-J. and Chang, G. J., ‘Isometric-path numbers of block graphs’, Inform. Process. Lett. 93 (2005), 99–102.Google Scholar
Pan, J.-J. and Chang, G. J., ‘Isometric path numbers of graphs’, Discrete Math. 306 (2006), 2091–2096.Google Scholar
Payne, M. and Wood, D. R., ‘On the general position subset selection problem’, SIAM J. Discrete Math. 27 (2013), 1727–1733.Google Scholar
Pěgřímek, D. and Gregor, P., ‘Hamiltonian laceability of hypercubes without isometric subgraphs’, Graphs Combin. 32 (2016), 2591–2624.Google Scholar
Polat, N., ‘On isometric subgraphs of infinite bridged graphs and geodesic convexity’, Discrete Math. 244 (2002), 399–416.Google Scholar
Por, A. and Wood, D. R., ‘No-three-in-line-in-3D’, Algorithmica 47 (2007), 481–488.Google Scholar
Shpectorov, S. V., ‘Distance-regular isometric subgraphs of the halved cubes’, European J. Combin. 19 (1998), 119–136.Google Scholar