Hostname: page-component-77c89778f8-cnmwb Total loading time: 0 Render date: 2024-07-16T21:54:10.621Z Has data issue: false hasContentIssue false
  • English
  • Français

Free algebra structure: categorical algebras

Published online by Cambridge University Press:  17 April 2009

H. G. Moore
H. G. Moore
Affiliation:
Brigham Young University, Provo, Utah, USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

One of the more important concepts in the study of universal algebras is that of a free algebra. It is our purpose in this communication to describe the structure of the free algebra Kk(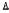) of k generators (k a positive integer) determined by a categorical algebra, and to indicate how this information encompasses results in such diverse areas as the study of Post algebras, boolean rings, p-rings, pk-rings, finite commutative rings with unity, etc.

A finite algebra 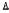is called categorical if every algebra in its equational class is isomorphic to a sub-direct power of A. If 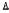has n elements, permutable identities, no non-identical automorphism and exactly m distinct one-element subalgebras, then .

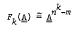Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 3 , Issue 2 , October 1970 , pp. 207 - 215
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Astromoff, Andrew, “Some structure theorems for primal and categorical algetras”, Math. Z. 87 (1965), 365–377.CrossRefGoogle Scholar
[2]Birkhoff, Garrett, Lattice theory (Colloquium Publ. 25, Amer. Math. Soc., Providence, Rhode Island, 3rd ed., 1967).Google Scholar
[3]Foster, Alfred L., “Generalized ‘boolean’ theory of universal algebra, Part I”, Math. Z. 58 (1953), 306–336. “Generalized ‘boolean’ theory of universal algebra, Part II”, Math. Z. 59 (1953), 191–199.CrossRefGoogle Scholar
[4]Foster, Alfred L., “On the finiteness of free (universal) algebras”, Proc. Amer. Math. Soc. 7 (1956), 1011–1013.CrossRefGoogle Scholar
[5]Foster, Alfred L. and Pixley, Alden, “Semi-categorical algebras, I”, Math. Z. 83 (1964), 147–169.CrossRefGoogle Scholar
[6]Grätzer, George, Universal algebra (Van Nostrand, Princeton, New Jersey; Toronto, London, Melbourne, 1968).Google Scholar
[7]Moore, H.G. and Yaqub, Adil, “An existence theorem for semi-primal algebras”, Ann. Scuola Norm. Sup. Pisa. (3) 22 (1968), 147–169.Google Scholar
[8]Moore, H.G. and Yaqub, Adil, “On the structure of certain free algebras”, Math. Japon. 14 (1969), 105–110.Google Scholar
[9]Wade, L.I., “Post algebras and rings”, Duke Math. J. 12 (1945), 389–395.CrossRefGoogle Scholar
[10]Yaqub, Adil, “Semi-primal categorical independent algebras”, Math. Z. 93 (1966), 395–403.CrossRefGoogle Scholar