Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
KOZLOWSKI, WOJCIECH M.
2018.
MONOTONE LIPSCHITZIAN SEMIGROUPS IN BANACH SPACES.
Journal of the Australian Mathematical Society,
Vol. 105,
Issue. 3,
p.
417.
Bin Dehaish, Buthinah A.
and
Khamsi, Mohamed A
2018.
Fibonacci–Mann Iteration for Monotone Asymptotically Nonexpansive Mappings in Modular Spaces.
Symmetry,
Vol. 10,
Issue. 10,
p.
481.
Aggarwal, Sajan
and
Uddin, Izhar
2019.
Convergence and stability of Fibonacci-Mann iteration for a monotone non-Lipschitzian mapping.
Demonstratio Mathematica,
Vol. 52,
Issue. 1,
p.
388.
Bin Dehaish, Buthinah A.
2019.
The Fibonacci–Mann iteration for monotone asymptotically pointwise nonexpansive mappings.
Journal of Fixed Point Theory and Applications,
Vol. 21,
Issue. 1,
Bachar, Mostafa
and
Khamsi, Mohamed Amine
2019.
Approximations of Fixed Points in the Hadamard Metric Space CATp(0).
Mathematics,
Vol. 7,
Issue. 11,
p.
1088.
Chaira, Karim
Kabil, Mustapha
Kamouss, Abdessamad
and
Lazaiz, Samih
2019.
Best Proximity Points for Monotone Relatively Nonexpansive Mappings in Ordered Banach Spaces.
Axioms,
Vol. 8,
Issue. 4,
p.
121.
Gürsoy, Faik
Khan, Abdul Rahim
Ertürk, Müzeyyen
and
Karakaya, Vatan
2019.
Weak $$w^{2}$$ w 2 -stability and data dependence of Mann iteration method in Hilbert spaces.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 113,
Issue. 1,
p.
11.
Malih, Sabah Hassan
and
Abed, Salwa Salman
2019.
Approximating random fixed points under a new iterative sequence.
Journal of Interdisciplinary Mathematics,
Vol. 22,
Issue. 8,
p.
1407.
Malih, Sabah Hassan
and
Abed, Salwa Salman
2021.
Convergence of random iterative scheme to a common random fixed points.
Journal of Physics: Conference Series,
Vol. 1963,
Issue. 1,
p.
012113.
Alfuraidan, M. R.
Khamsi, M. A.
and
Kozlowski, W. M.
2021.
Advances in Metric Fixed Point Theory and Applications.
p.
217.
Malih, Sabah Hassan
and
Abed, Salwa Salman
2021.
Convergence and stability of some random iterative schemes.
Journal of Physics: Conference Series,
Vol. 1963,
Issue. 1,
p.
012112.
Malih, Sabah Hassan
2021.
Random Fixed Point on Ishikawa Random Iteration Under Fibonacci Sequence.
Journal of Physics: Conference Series,
Vol. 1879,
Issue. 3,
p.
032044.
Malih, Sabah Hassan
2021.
Common Fixed Point for a Pair of Asymptotically Nonexpansive and Multivalued Mapping Under Fibonacci Iteration Sequence in CAT (0) Space.
Journal of Physics: Conference Series,
Vol. 1897,
Issue. 1,
p.
012061.
Malih, Sabah Hassan
2021.
Random fixed point for random Fibonacci Noor iteration scheme.
Journal of Interdisciplinary Mathematics,
Vol. 24,
Issue. 3,
p.
775.
Malih, Sabah Hassan
2021.
Fixed point theorems of modified Mann and Ishikawa iterations.
Journal of Interdisciplinary Mathematics,
Vol. 24,
Issue. 5,
p.
1093.
Özgür, Nihal
Antal, Swati
Tomar, Anita
and
Liu, Jia-Bao
2022.
Julia and Mandelbrot Sets of Transcendental Function via Fibonacci-Mann Iteration.
Journal of Function Spaces,
Vol. 2022,
Issue. ,
p.
1.
Tomar, Anita
Kumar, Vipul
Rana, Udhamvir Singh
and
Sajid, Mohammad
2023.
Fractals as Julia and Mandelbrot Sets of Complex Cosine Functions via Fixed Point Iterations.
Symmetry,
Vol. 15,
Issue. 2,
p.
478.
Antal, Swati
Özgür, Nihal
Tomar, Anita
and
Gdawiec, Krzysztof
2024.
Fractal generation via generalized Fibonacci–Mann iteration with s-convexity.
Indian Journal of Pure and Applied Mathematics,
Sharma, Saurabh
Tomar, Anita
and
Padaliya, Sanjay Kumar
2025.
On the evolution and importance of the Fibonacci sequence in visualization of fractals.
Chaos, Solitons & Fractals,
Vol. 191,
Issue. ,
p.
115851.
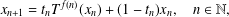 $$\begin{eqnarray}x_{n+1}=t_{n}T^{f(n)}(x_{n})+(1-t_{n})x_{n},\quad n\in \mathbb{N},\end{eqnarray}$$
$$\begin{eqnarray}x_{n+1}=t_{n}T^{f(n)}(x_{n})+(1-t_{n})x_{n},\quad n\in \mathbb{N},\end{eqnarray}$$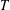 $T$ is a monotone asymptotically nonexpansive self-mapping defined on a closed bounded and nonempty convex subset of a uniformly convex Banach space and
$T$ is a monotone asymptotically nonexpansive self-mapping defined on a closed bounded and nonempty convex subset of a uniformly convex Banach space and 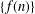 $\{f(n)\}$ is the Fibonacci integer sequence. We obtain a weak convergence result in
$\{f(n)\}$ is the Fibonacci integer sequence. We obtain a weak convergence result in 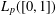 $L_{p}([0,1])$, with
$L_{p}([0,1])$, with 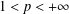 $1<p<+\infty$, using a property similar to the weak Opial condition satisfied by monotone sequences.
$1<p<+\infty$, using a property similar to the weak Opial condition satisfied by monotone sequences.